题目内容
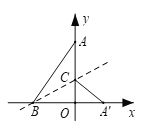
【题目】如图,一次函数y=mx+2m+3的图像与y=-![]() x的图像交于点C,且点C的横坐标为-3,与x轴、y轴分别交于点A、点B.
x的图像交于点C,且点C的横坐标为-3,与x轴、y轴分别交于点A、点B.
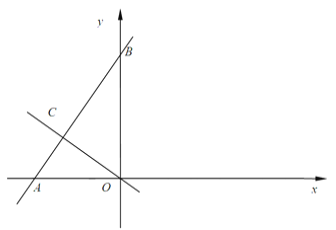
(1)求m的值与AB的长;
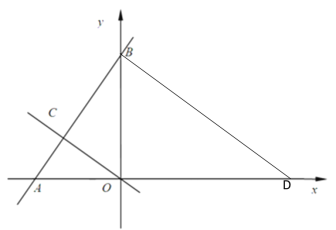
(2)若点D(9,0),连结BD,求证△ABD为直角三角形.
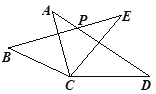
(3)在y轴上是否存在点P,使得△ABP为等腰三角形,若存在请求出P的坐标,若不存在,请说明理由.
【答案】(1)m=![]() ;
;![]() ;(2)见解析;(3)存在,(6-
;(2)见解析;(3)存在,(6-![]() ,0)或(6+
,0)或(6+![]() ,0)或(0,﹣6)或(0,
,0)或(0,﹣6)或(0,![]() ).
).
【解析】
(1)先求出C点坐标,然后将C点坐标代入一次函数解析式中,即可求出m,然后分别求出A、B两点坐标,根据勾股定理即可求出AB的长;
(2)先计算出AD的长,然后根据勾股定理求出BD,再根据勾股定理的逆定理,即可证出△ABD为直角三角形;
(3)根据等腰三角形的腰的情况分类讨论,然后分别求出点P的坐标即可.
解:(1)将x=-3代入y=-![]() x中得:y=
x中得:y=![]()
∴C点坐标为:(-3,![]() )
)
将C点坐标代入y=mx+2m+3中,得:![]() =-3m+2m+3
=-3m+2m+3
解得:m=![]()
∴一次函数的解析式为:y=![]() x+6
x+6
当x=0时,y=6,当y=0时,x=﹣4
∴B点坐标为(0,6),点A的坐标为(﹣4,0)
∴OB=6,OA=4
根据勾股定理:AB=![]() ;
;
(2)∵点A的坐标为(﹣4,0),点D点坐标为(9,0)
∴AD=9-(﹣4)=13
根据勾股定理:BD=![]()
∵AB2+BD2=169,AD2=169
∴AB2+BD2= AD2
∴△ABD为直角三角形
(3)存在,
①若BP=BA时
如下图所示,此时也有两种情况,
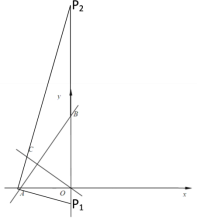
∵AB=![]() ,点B的坐标为(0,6)
,点B的坐标为(0,6)
∴P1的坐标为(6-![]() ,0),P2的坐标为(6+
,0),P2的坐标为(6+![]() ,0);
,0);
②若AB=AP时,如下图所示:
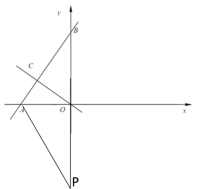
∵AO⊥BP
∴BO=OP
∴此时点P的坐标为(0,﹣6);
③若BP=AP时,如下图所示
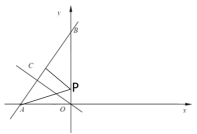
设OP=x,则PB=PA=6-x
根据勾股定理:![]()
即:![]()
解得:![]()
此时P点坐标为(0,![]() )
)
综上所述:P点坐标为:(6-![]() ,0)或(6+
,0)或(6+![]() ,0)或(0,﹣6)或(0,
,0)或(0,﹣6)或(0,![]() ).
).

 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
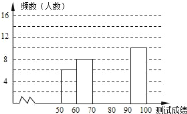
波波熊暑假作业江西人民出版社系列答案【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
(1)①频数分布表中a的值为;②若测试成绩不低于80分为优秀,则本次测试的优秀率是;③将频数分布直方图补充完整;
(2)第5组10名同学中,有4名男同学(用A,B,C,D表示),现将这4名同学分成两组(每组2人)进行对抗练习,求A与B两名男同学能分在同一组的概率.
组别 | 成绩x分 | 频数(人数) |
第1组 | 50≤x<60 | 6 |
第2组 | 60≤x<70 | 8 |
第3组 | 70≤x<80 | 14 |
第4组 | 80≤x<90 | a |
第5组 | 90≤x<100 | 10 |