Question

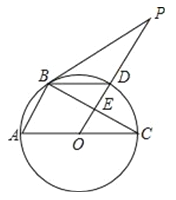
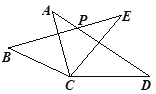
【题目】如图，在△ACD和△BCE中， AC＝BC，AD＝BE，CD＝CE，∠ACE＝55°，∠BCD＝155°，AD与BE相交于点P，则∠BPD的度数为（　　）

A.110°B.125°C.130°D.155°

Answer 1

【答案】C

【解析】

根据AC＝BC，AD＝BE，CD＝CE得出，据此求出∠ACB度数，再利用三角形内角和求得∠APB=∠ACB，进一步求出答案即可.

在△ACD与△BCE中，

∵AC＝BC，AD＝BE，CD＝CE，

∴，

∴∠ACD=∠BCE，∠A=∠B，

∴∠BCA＋∠ACE=∠ACE＋∠ECD，

∴∠ACB=∠ECD=(∠BCD－∠ACE)=50°，

∵∠B＋∠ACB=∠A＋∠APB，

∴∠APB=∠ACB=50°，

∴∠BPD=180°－50°=130°.

所以答案为C选项.