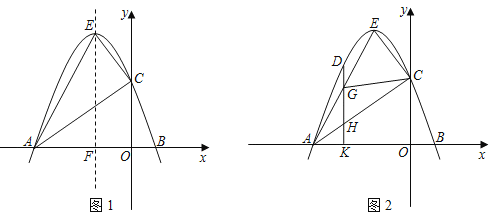ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§“Μ¥ΈΚ· ΐyΘΫ©¹x+bΒΡΆΦœσ”κΖ¥±»άΐΚ· ΐyΘΫ©¹![]() ‘ΎΒΎΕΰœσœόΡΎΒΡΆΦœσœύΫΜ”ΎΒψAΘ§”κx÷αΒΡΗΚΑκ÷αΫΜ”ΎΒψBΘ§”κy÷αΒΡΗΚΑκ÷αΫΜ”ΎΒψCΘ°
‘ΎΒΎΕΰœσœόΡΎΒΡΆΦœσœύΫΜ”ΎΒψAΘ§”κx÷αΒΡΗΚΑκ÷αΫΜ”ΎΒψBΘ§”κy÷αΒΡΗΚΑκ÷αΫΜ”ΎΒψCΘ°
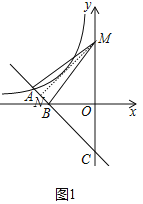
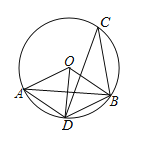
Θ®1Θ©«σΓœBCOΒΡΕ» ΐΘΜ
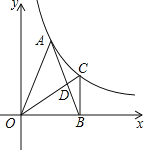
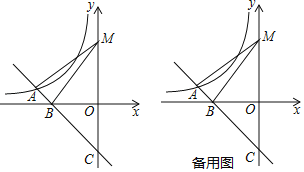
Θ®2Θ©»τy÷α…œ“ΜΒψMΒΡΉίΉχ±ξ «4Θ§«“AMΘΫBMΘ§«σΒψAΒΡΉχ±ξΘΜ
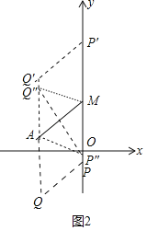
Θ®3Θ©‘ΎΘ®2Θ©ΒΡΧθΦΰœ¬Θ§»τΒψP‘Ύy÷α…œΘ§ΒψQ «ΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–ΒΡ“ΜΒψΘ§Β±“‘ΒψAΓΔMΓΔPΓΔQΈΣΕΞΒψΒΡΥΡ±Ώ–Έ «Νβ–Έ ±Θ§«κ÷±Ϋ”–¥≥ωΒψQΒΡΉχ±ξΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©ΓœBCOΘΫ45ΓψΘΜΘ®2Θ©A(©¹4Θ§1)ΘΜΘ®3Θ©ΒψQΉχ±ξΈΣ(©¹4Θ§©¹4)Μρ(©¹4Θ§6)Μρ(©¹4Θ§![]() )Μρ(4Θ§1)Θ°
)Μρ(4Θ§1)Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©÷ΛΟςΓςOBC «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΦ¥Ω…ΫβΨωΈ ΧβΘΜ
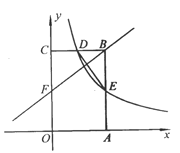
Θ®2Θ©»γΆΦ1÷–Θ§ΉςMNΓΆAB”ΎNΘ°ΗυΨί“Μ¥ΈΚ· ΐ«σ≥ωΫΜΒψNΒΡΉχ±ξΘ§”Οb±μ ΨΒψAΉχ±ξΘ§‘Όάϊ”Ο¥ΐΕ®œΒ ΐΖ®Φ¥Ω…ΫβΨωΈ ΧβΘΜ
Θ®3Θ©Ζ÷ΝΫ÷÷«ι–ΈΘΚΔΌΒ±Νβ–Έ“‘AMΈΣ±Ώ ±Θ§ΔΎΒ±AMΈΣΝβ–ΈΒΡΕ‘Ϋ«œΏ ±Θ§Ζ÷±π«σΫβΦ¥Ω…Θ°
Θ®1Θ©ΓΏ“Μ¥ΈΚ· ΐyΘΫ©¹x+bΒΡΆΦœσΫΜx÷α”ΎBΘ§ΫΜy÷α”ΎCΘ§‘ρB(bΘ§0)Θ§CΘ®0Θ§bΘ©Θ§
ΓύOBΘΫOCΘΫ©¹bΘ§
ΓΏΓœBOCΘΫ90Γψ
ΓύΓςOBC «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§
ΓύΓœBCOΘΫ45ΓψΘ°
Θ®2Θ©»γΆΦ1÷–Θ§ΉςMNΓΆAB”ΎNΘ§
ΓΏMΘ®0Θ§4Θ©Θ§MNΓΆACΘ§÷±œΏACΒΡΫβΈω ΫΈΣΘΚyΘΫ©¹x+bΘ§
Γύ÷±œΏMNΒΡΫβΈω ΫΈΣΘΚyΘΫx+4Θ§
ΝΣΝΔ![]() Θ§ΫβΒΟΘΚ
Θ§ΫβΒΟΘΚ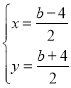 Θ§
Θ§
ΓύN(![]() Θ§
Θ§![]() )Θ§
)Θ§
ΓΏMAΘΫMBΘ§MNΓΆABΘ§
ΓύNAΘΫBNΘ§…ηA(mΘ§n)Θ§
‘ρ”–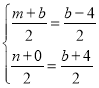 Θ§ΫβΒΟΘΚ
Θ§ΫβΒΟΘΚ![]() Θ§
Θ§
ΓύA(©¹4Θ§b+4)Θ§
ΓΏΒψA‘ΎyΘΫ©¹![]() …œΘ§
…œΘ§
Γύ©¹4Θ®b+4Θ©ΘΫ©¹4Θ§
ΓύbΘΫ©¹3Θ§
ΓύAΘ®©¹4Θ§1Θ©ΘΜ
Θ®3Θ©»γΆΦ2÷–Θ§
”…Θ®2Θ©Ω…÷ΣA(©¹4Θ§1)Θ§M(0Θ§4)Θ§
ΓύAMΘΫ![]() ΘΫ5Θ§
ΘΫ5Θ§
Β±Νβ–Έ“‘AMΈΣ±Ώ ±Θ§AQΘΫAQΓδΘΫ5Θ§AQΓΈOMΘ§Ω…ΒΟQ(©¹4Θ§©¹4)Θ§QΓδ(©¹4Θ§6)Θ§
Β±AΘ§QΙΊ”Ύy÷αΕ‘≥Τ ±Θ§“≤¬ζΉψΧθΦΰΘ§¥Υ ±Q(4Θ§1)Θ§
Β±AMΈΣΝβ–ΈΒΡΕ‘Ϋ«œΏ ±Θ§…ηPΓε(0Θ§b)Θ§
‘ρ”–Θ®4©¹bΘ©2ΘΫ42+Θ®b©¹1Θ©2Θ§
ΓύbΘΫ©¹![]() Θ°
Θ°
ΓύAQΓεΘΫMPΓεΘΫ![]() Θ§
Θ§
ΓύQΓε(©¹4Θ§![]() )Θ§
)Θ§
Ήέ…œΥυ ωΘ§¬ζΉψΧθΦΰΒΡΒψQΉχ±ξΈΣ(©¹4Θ§©¹4)Μρ(©¹4Θ§6)Μρ(©¹4Θ§![]() )Μρ(4Θ§1)Θ°
)Μρ(4Θ§1)Θ°