题目内容
【题目】合肥百大集团新进了40台空调机，60台电冰箱，计划调配给下属的甲、乙两个连锁店销售，其中70台给甲连锁店，30台给乙连锁店．两个连锁店销售这两种电器每台的利润（元）如下表：
空调机 | 电冰箱 | |
甲连锁店 | 200 | 170 |
乙连锁店 | 160 | 150 |
设集团调配给甲连锁店x台空调机，集团卖出这100台电器的总利润为y（元）．
（1）求y关于x的函数关系式，并求出x的取值范围；
（2）为了促销，集团决定仅对甲连锁店的空调机每台让利a元销售，其他的销售利润不变，并且让利后每台空调机的利润仍然高于甲连锁店销售的每台电冰箱的利润，问该集团应该如何设计调配方案，才能使总利润达到最大？
【答案】（1）y=20x+16800 (10≤x≤40，且
为整数)；（2）当0＜a＜20时，x=40，即调配给甲连锁店空调机40台，电冰箱30台，乙连锁店空调0台，电冰箱30台；当a=20时，x的取值在10≤x≤40内的所有方案利润相同； 当20＜a＜30时，x=10，即调配给甲连锁店空调机10台，电冰箱60台，乙连锁店空调30台，电冰箱0台.
【解析】试题分析：（1）首先设调配给甲连锁店电冰箱（70-x）台，调配给乙连锁店空调机（40-x）台，电冰箱60-（70-x）=（x-10）台，列出不等式组求解即可；
（2）由（1）可得几种不同的分配方案；依题意得出y与a的关系式，解出不等式方程后可得出使利润达到最大的分配方案．
试题解析：（1）由题意可知，调配给甲连锁店电冰箱（70-x）台，
调配给乙连锁店空调机（40-x）台，电冰箱为60-（70-x）=（x-10）台，
则y=200x+170（70-x）+160（40-x）+150（x-10），
即y=20x+16800．
∵
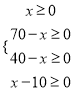
∴10≤x≤40．
∴y=20x+16800（10≤x≤40）；
（2）由题意得：y=（200-a）x+170（70-x）+160（40-x）+150（x-10），
即y=（20-a）x+16800．
∵200-a＞170，
∴a＜30．
当0＜a＜20时，20-a＞0，函数y随x的增大而增大，
故当x=40时，总利润最大，即调配给甲连锁店空调机40台，电冰箱30台，乙连锁店空调0台，电冰箱30台；
当a=20时，x的取值在10≤x≤40内的所有方案利润相同；
当20＜a＜30时，20-a＜0，函数y随x的增大而减小，
故当x=10时，总利润最大，即调配给甲连锁店空调机10台，电冰箱60台，乙连锁店空调30台，电冰箱0台．
