题目内容
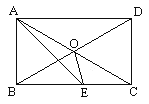
【题目】已知:如图,O是矩形ABCD对角线的交点,AE平分∠BAD,∠AOD=120°,求∠AEO的度数.
【答案】30°
【解析】
根据矩形的性质可得OB=OC,AD∥BC,∠ABC=∠BAD=90°,又由AE平分∠BAD,∠AOD=120°,即可求得∠OBC和∠AEB的度数,以及AB=BE ,AB=OA=OB,即可得OB=BE,∠BOE=∠BEO,即可求得∠OEB的度数
解:∵四边形ABCD是矩形,
∴AD∥BC,∠ABC=∠BAD=90°,
AC=BD,OB=0.5BD,OC=0.5AC,
∴OB=OC,
∴∠OBC=∠OCB,
∵∠BOC=∠AOD=120°,
∴∠OBC=30°,
∵AE平分∠BAD,
∴∠BAE=∠EAD=45°,
∴∠AEB=∠EAD=∠BAE=45°,
∴AB=BE,
∵∠AOD=120°,
∴∠AOB=60°,
∴AB=OA=OB,
∴OB=BE,
∴∠BOE=∠BEO,
∴∠OEB=75°,
∴∠AEO=∠OEB-∠AEB=75°-45°=30°.

练习册系列答案
相关题目
【题目】公园的门票价格规定如下表:
购票张数 | 1 到 50 张 | 51 到 100 张 | 101 到 150张 | 150 张以上 |
每张票的价格 | 12 元 | 10 元 | 8 元 | 超过 150 张的部分 7 元 |
某校七年级(1)(2)两个班共 104 人,其中(1)班 40 多人,不足 50 人,经估算,如果两个班都以班为单位购票,则一共应付 1136 元,问:
(1)若两班联合起来作为一个团体购票,可省多少钱?
(2)两班学生各有多少人?
(3)若七年级(3)班有 n 人(46<n<55)与(1),(2)班一起去游园,某商家赞助,支付三个班的所有门票费,则该商家最少花费 元(用含 n 的式子表示)