题目内容
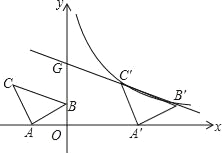
【题目】如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(﹣2,0),B(0,1).
(1)求点C的坐标;
(2)将△ABC沿x轴的正方向平移,在第一象限内B、C两点的对应点B'、C'正好落在某反比例函数图象上.请求出这个反比例函数和此时的直线B'C'的解析式.
(3)若把上一问中的反比例函数记为y1,点B′,C′所在的直线记为y2,请直接写出在第一象限内当y1<y2时x的取值范围.
【答案】(1)C(﹣3,2);(2)y1=![]() , y2=﹣
, y2=﹣![]() x+3; (3)3<x<6.
x+3; (3)3<x<6.
【解析】分析:
(1)过点C作CN⊥x轴于点N,由已知条件证Rt△CAN≌Rt△AOB即可得到AN=BO=1,CN=AO=2,NO=NA+AO=3结合点C在第二象限即可得到点C的坐标;
(2)设△ABC向右平移了c个单位,则结合(1)可得点C′,B′的坐标分别为(﹣3+c,2)、(c,1),再设反比例函数的解析式为y1=![]() ,将点C′,B′的坐标代入所设解析式即可求得c的值,由此即可得到点C′,B′的坐标,这样用待定系数法即可求得两个函数的解析式了;
,将点C′,B′的坐标代入所设解析式即可求得c的值,由此即可得到点C′,B′的坐标,这样用待定系数法即可求得两个函数的解析式了;
(3)结合(2)中所得点C′,B′的坐标和图象即可得到本题所求答案.
详解:
(1)作CN⊥x轴于点N,
∴∠CAN=∠CAB=∠AOB=90°,
∴∠CAN+∠CAN=90°,∠CAN+∠OAB=90°,
∴∠CAN=∠OAB,
∵A(﹣2,0)B(0,1),
∴OB=1,AO=2,
在Rt△CAN和Rt△AOB,
∵ ,
,
∴Rt△CAN≌Rt△AOB(AAS),
∴AN=BO=1,CN=AO=2,NO=NA+AO=3,
又∵点C在第二象限,
∴C(﹣3,2);
(2)设△ABC沿x轴的正方向平移c个单位,则C′(﹣3+c,2),则B′(c,1),
设这个反比例函数的解析式为:y1=![]() ,
,
又点C′和B′在该比例函数图象上,把点C′和B′的坐标分别代入y1=![]() ,得﹣6+2c=c,
,得﹣6+2c=c,
解得c=6,即反比例函数解析式为y1=![]() ,
,
此时C′(3,2),B′(6,1),设直线B′C′的解析式y2=mx+n,
∵![]() ,
,
∴  ,
,
∴直线C′B′的解析式为y2=﹣![]() x+3;
x+3;
(3)由图象可知反比例函数y1和此时的直线B′C′的交点为C′(3,2),B′(6,1),
∴若y1<y2时,则3<x<6.