题目内容
【题目】如图①,四边形![]() 是正方形,点
是正方形,点![]() 是边
是边![]() 的中点,
的中点,![]() ,且
,且![]() 交正方形的外角平分线
交正方形的外角平分线![]() 于点
于点![]() 请你认真阅读下面关于这个图形的探究片段,完成所提出的问题.
请你认真阅读下面关于这个图形的探究片段,完成所提出的问题.
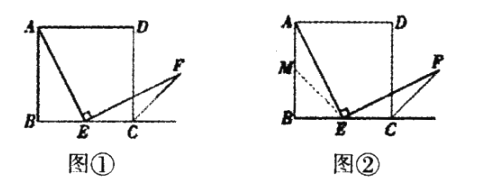
(1)探究1:小强看到图①后,很快发现![]() 这需要证明AE和EF所在的两个三角形全等,但△ABE和△ECF显然不全等(个直角三角形,一个钝角三角形)考虑到点E是边BC的中点,因此可以选取AB的中点M(如图②),连接EM后尝试着去证明
这需要证明AE和EF所在的两个三角形全等,但△ABE和△ECF显然不全等(个直角三角形,一个钝角三角形)考虑到点E是边BC的中点,因此可以选取AB的中点M(如图②),连接EM后尝试着去证明![]() 就行了.随即小强写出了如下的证明过程:
就行了.随即小强写出了如下的证明过程:
证明:如图②,取AB的中点M,连接EM.
∵![]()
∴![]()
又∵![]()
∴![]()
∵点E、M分别为正方形的边BC和AB的中点,
∴![]()
∴![]() 是等腰直角三角形,
是等腰直角三角形,![]()
∴![]()
又∵![]() 是正方形外角的平分线,
是正方形外角的平分线,
∴![]() ,∴
,∴![]()
∴![]()
∴![]() ,
,
∴![]()
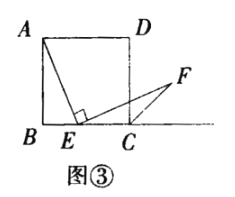
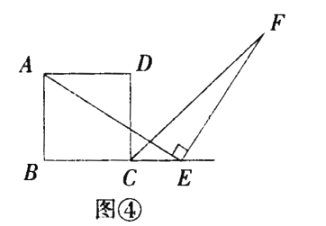
(2)探究2:小强继续探索,如图③,若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点”,其余条件不变,发现AE=EF仍然成立小强进一步还想试试,如图④,若把条件“点E是边BC的中点”为“点E是边BC延长线上的一点”,其余条件仍不变,那么结论AE=EF仍然成立请你选择图③或图④中的一种情况写出证明过程给小强看.
【答案】见解析
【解析】
在AB上截取AM=EC,连接ME,然后证明∠EAM=FEC,∠AME=∠ECF=135°,再利用“角边角”证明△AEM和△EFC全等,然后根据全等三角形对应边相等即可证明;
(2)探究2:选择图③进行证明:
证明:如图③在![]() 上截取
上截取![]() ,连接
,连接![]() .
.

由(1)知∠EAM=∠FEC,
∵AM=EC,AB=BC,
∴BM=BE,
∴∠BME=45°,
∴∠AME=∠ECF=135°,
∵∠AEF=90°,
∴∠FEC+∠AEB=90°,
又∵∠EAM+∠AEB=90°,
∴∠EAM=∠FEC,
在△AEM和△EFC中,
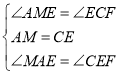
∴△AEM≌△EFC(ASA),
∴AE=EF;

练习册系列答案
相关题目