题目内容
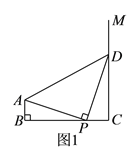
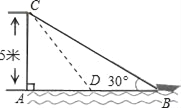
【题目】如图,在离水面高度为5m的岸上有人用绳子拉船靠岸,开始绳子与水面的夹角为30°,此人以每秒0.5m的速度收绳.
(1)8秒后船向岸边移动了多少米?
(2)写出还没收的绳子的长度S米与收绳时间t秒的函数关系式.

【答案】(1)![]() (m);(2)S=10﹣0.5t(0≤t≤10).
(m);(2)S=10﹣0.5t(0≤t≤10).
【解析】【试题分析】
(1)假设8秒后,船到达D位置,连接CD,
在Rt△ACB中,AC=5m,∠CBA=30°,根据30度所对的直角边是斜边的一半,得:CB=2AC=10m;此人以每秒0.5m的速度收绳,则8秒后收回的绳子长为:0.5×8=4m,
则CD=10﹣4=6(m);在Rt△ACD中,根据勾股定理得: AD=![]() (m);在Rt△ACB中,根据勾股定理得: AB=
(m);在Rt△ACB中,根据勾股定理得: AB=![]() (m),则BD=AB﹣AD=
(m),则BD=AB﹣AD=![]() (m);即8秒后船向岸边移动了
(m);即8秒后船向岸边移动了![]() 米.
米.
(2)原来绳子的长度为10米,以每秒0.5m的速度收绳,则t秒后剩下的绳长为(10-0.5t)米,即S=10﹣0.5t,由于绳长至少为5米,则要求0≤t≤10.
【试题解析】
(1)假设8秒后,船到达D位置,连接CD,
∵AC=5m,∠CBA=30°,
∴CB=2AC=10m,
此人以每秒0.5m的速度收绳,则8秒后收回的绳子长为:0.5×8=4m,
∴CD=10﹣4=6(m),
在Rt△ACD中: AD=![]() (m),
(m),
在Rt△ACB中:AB=![]() (m),
(m),
则BD=AB﹣AD=![]() (m);
(m);

(2)S=10﹣0.5t(0≤t≤10).

练习册系列答案
相关题目