��Ŀ����
����Ŀ������ij���ճ�Ϊ��ϱ������ˣ������һ��ɱ�Ϊ20Ԫ�M���Ĺ���ƷͶ���г������������������飬�õ��������ݣ�
���۵���x��Ԫ/���� | �� | 30 | 40 | 50 | 60 | �� |
ÿ��������y������ | �� | 500 | 400 | 300 | 200 | �� |
��1�����ϱ���x��y�ĸ����Ӧֵ��Ϊ������꣬�������ƽ��ֱ������ϵ�������Ӧ�ĵ㣬����y��x�ĺ�����ϵ�������������ϵʽ�� 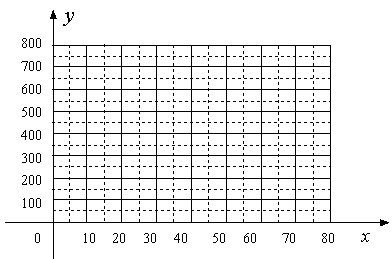
��2�������۵��۶�Ϊ����ʱ�����ճ������ù���Ʒÿ���õ����������������Ƕ��٣�������=�����ܼ۩��ɱ��ܼۣ�
��3��������۲��Ź涨���ù���Ʒ���۵�����߲��ܳ���45Ԫ/������ô���۵��۶�Ϊ����ʱ�����ճ������ù���Ʒÿ���õ��������
���𰸡�
��1���⣺��ͼ��ʾ��

��ͼ�ɲ���y��x��һ�κ�����ϵ��
�����һ�κ���Ϊy=kx+b��k��0��
�����һ�κ�����ͼ����30��500��
��40��400�������㣬
�� ![]() ���
��� ![]()
�ຯ����ϵʽ�ǣ�y=��10x+800��20��x��80��
��2���⣺�蹤�ճ������ù���Ʒÿ���õ�������WԪ���������
W=��x��20������10x+800��
=��10x2+1000x��16000
=��10��x��50��2+9000����20��x��80��
�൱x=50ʱ��W�����ֵ9000��
���ԣ������۵��۶�Ϊ50Ԫ�M��ʱ�����ճ������ù���Ʒÿ���õ�����������������9000Ԫ
��3���⣺���ں���W=��10��x��50��2+9000����x��45ʱ��
W��ֵ����xֵ�����������
�����۵��۶�Ϊ45Ԫ�M��ʱ�����ճ������ù���Ʒÿ���õ��������
����������1����㣬��ͼ�ɲ���y��x��һ�κ�����ϵ����ѡ���������ʽ������֤�������ȷ�ԣ���2������=�����ܼ۩��ɱ��ܼ�=������������������ݴ˵ñ���ʽ��������������ֵ����3�������Ա�����ȡֵ��Χ��Ϻ���ͼ����

 ��У����ϵ�д�
��У����ϵ�д�����Ŀ��ij������˾�ƻ�װ�˼ס��ҡ������ּҵ絽ũ������(�涨ÿ���������涨��������ÿ������ֻ��װͬһ�ּҵ�)���±���ʾΪװ�˼ס��ҡ������ּҵ��̨��������
�� | �� | �� | |
ÿ��������װ�˵�̨�� | 40 | 20 | 30 |
ÿ̨�ҵ�ɻ�����(��Ԫ) | 0.05 | 0.07 | 0.04 |
(1)����8������װ���ҡ������ּҵ�190̨��A����������װ���ҡ�������������������
(2)�ƻ���20������װ�˼ס��ҡ������ּҵ�720̨��B����������ΰ���װ������ʹ��˾���36.6��Ԫ������