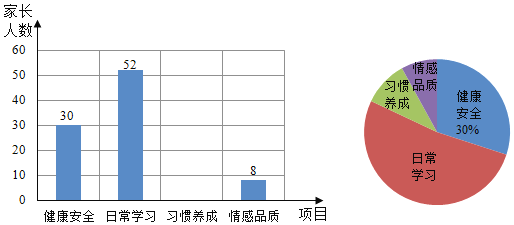
题目内容
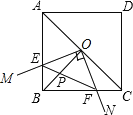
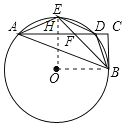
【题目】如图,Rt△ABC中,∠C=90°,点A、B、D、E在圆O上,弧AE=弧DE,连接BE交AE于F,∠BFC=45°,EF=2,BF=4.
(1)求AE的长;
(2)求证:BC是圆O的切线;
(3)求tan∠ABC.

【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() .
.
【解析】
(1)根据相似三角形的性质和判定即可得到答案;
(2)根据平行线的性质和圆切线的判定即可得到答案;
(3)根据三角函数和勾股定理即可得到答案.
解:(1)∵弧AE=弧DE
∴∠DAE=∠EBA,且∠AEF=∠AEB
∴△AEF∽△BEA
∴![]()
∴AE2=BEEF,且EF=2,BF=4.
∴AE2=2×6=12
∴![]()
(2)连接OE交AD于点H,连接OB,
∵△AEF∽△BEA
∴∠BAE=∠AFE=∠BFC=45°
∴∠BOE=90°,
∵![]() ,OE是半径
,OE是半径
∴OE⊥AD,且∠C=90°,
∴OE∥BC,且∠BOE=90°
∴∠OBC=90°,
即OB⊥BC,
∴BC是圆O的切线
(3)∵BF=4,∠C=90°,∠BFC=45°
∴CF=CB=2![]()
∵∠EHF=90°,EF=2,∠EFH=45°
∴EH=HF=![]()
∴AH=![]() =
=![]()
∴AC=AH+HF+CF=![]()
∴tan∠ABC=![]() =
=![]() =
=![]()

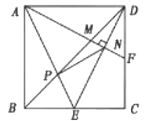
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 的中点,
的中点,![]() .将
.将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 度
度![]() ,角的两边分别交直线
,角的两边分别交直线![]() 于
于![]() 两点,设
两点,设![]() 点间的距离为
点间的距离为![]() ,
,![]() 两点间的距离为
两点间的距离为![]() .
.
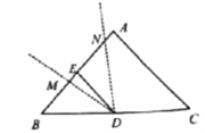
小涛根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究下面是小涛的探究过程,请补充完整.
的变化而变化的规律进行了探究下面是小涛的探究过程,请补充完整.
(1)列表:下表的已知数据是根据![]() 两点间的距离
两点间的距离![]() 进行取点、画图、测量,分别得到了 与 的几组对应值:
进行取点、画图、测量,分别得到了 与 的几组对应值:
| 0 | 0.30 | 0.50 | 1.00 | 1.50 | 2.00 | 2.50 |
| 3.00 | 3.50 | 3.68 | 3.81 | 3.90 | 3.93 | 4.10 |
| 2.88 | 2.81 | 2.69 | 2.67 | 2.80 | 3.15 | 3.85 | 5.24 | 6.01 | 6.71 | 7.27 | 7.44 | 8.87 |
请你通过计算,补全表格
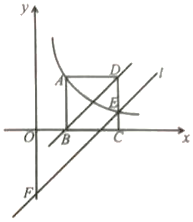
(2)描点、连线:在平面直角坐标系![]() 中,描出表中各组数值所对应的点
中,描出表中各组数值所对应的点![]() ,并画出函数
,并画出函数![]() 关于
关于![]() 的图象:
的图象:

(3)探究性质:随着自变量![]() 的不断增大,函数
的不断增大,函数![]() 的变化趋势:
的变化趋势:
(4)解决问题:当![]() 时,
时,![]() 的长度大约是____
的长度大约是____![]() (保留两位小数).
(保留两位小数).