Question

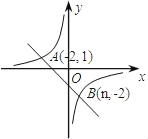
【题目】已知二次函数y=ax2+bx+c的图象如图所示,其对称轴为直线x=-1,给出下列结果: (1)b2>4ac. (2)abc>0. (3)2a+b=0.(4)a+b+c>0. (5)a-b+c<0.则正确的结论 ______(填序号)

Answer 1

【答案】（1）（4）（5）；

【解析】

抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．

（1）如图所示，二次函数与x轴有两个交点，所以b2-4ac＞0，则b2＞4ac．故（1）正确；
（2）、（3）如图所示，∵抛物线开口向上，所以a＞0，抛物线与y轴交点在负半轴上，
∴c＜0．
又

∴b=2a＞0，
∴abc＜0，2a-b＜0．
故（2）、（3）错误；
（4）如图所示，由图象可知当x=1时，y＞0，即a+b+c＞0．
故（4）正确；
（5）由图象可知当x=-1时，y＜0，即a-b+c＜0．
故（5）正确．
综上所述，正确的结论是（1）（4）（5）．