Question

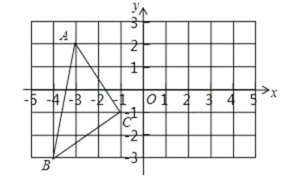
【题目】如图，在正方形网络中，△ABC的三个顶点都在格点上，点A、B、C的坐标分别为（－2，4）、（－2，0）、（－4，1），结合所给的平面直角坐标系解答下列问题：

（1）画出△ABC关于原点O对称的△A1B1C1.

（2）平移△ABC，使点A移动到点A2（0，2），画出平移后的△A2B2C2并写出点B2、C2的坐标.

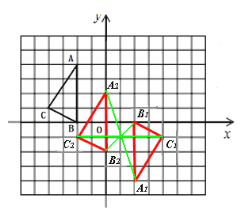
（3）在△ABC、△A1B1C1、△A2B2C2中，△A2B2C2与 成中心对称，其对称中心的坐标为 .

Answer 1

【答案】（1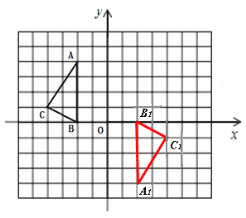）（2）平移后的△A2B2C2如图所示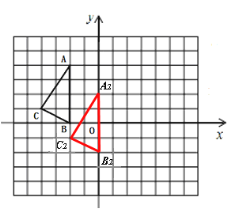点B2、C2的坐标分别为（0，－2），（－2，－1）（3）△A1B1C1；（1，－1）

【解析】解：（1）△ABC关于原点O对称的△A1B1C1如图所示：

（2）平移后的△A2B2C2如图所示：

点B2、C2的坐标分别为（0，－2），（－2，－1）。

（3）△A1B1C1；（1，－1）。

（1）根据中心对称的性质，作出A、B、C三点关于原点的对称点A1、B1、C1，连接即可。

（2）根据平移的性质，点A（－2，4）→A2（0，2），横坐标加2，纵坐标减2，所以将B（－2，0）、C（－4，1）横坐标加2，纵坐标减2得到B2（0，－2）、C2（－2，－1），连接即可。

（3）如图所示。