题目内容
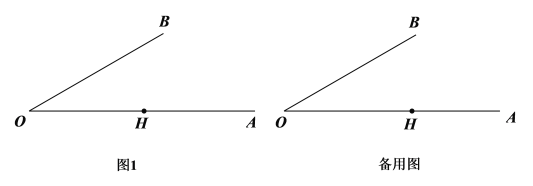
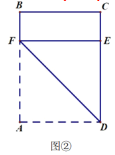
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 的中点,
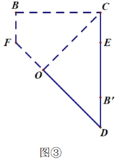
的中点,![]() .将
.将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 度
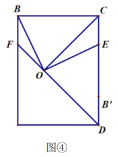
度![]() ,角的两边分别交直线
,角的两边分别交直线![]() 于
于![]() 两点,设
两点,设![]() 点间的距离为
点间的距离为![]() ,
,![]() 两点间的距离为
两点间的距离为![]() .
.
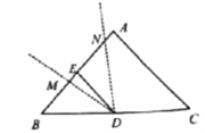
小涛根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究下面是小涛的探究过程,请补充完整.
的变化而变化的规律进行了探究下面是小涛的探究过程,请补充完整.
(1)列表:下表的已知数据是根据![]() 两点间的距离
两点间的距离![]() 进行取点、画图、测量,分别得到了 与 的几组对应值:
进行取点、画图、测量,分别得到了 与 的几组对应值:
| 0 | 0.30 | 0.50 | 1.00 | 1.50 | 2.00 | 2.50 |
| 3.00 | 3.50 | 3.68 | 3.81 | 3.90 | 3.93 | 4.10 |
| 2.88 | 2.81 | 2.69 | 2.67 | 2.80 | 3.15 | 3.85 | 5.24 | 6.01 | 6.71 | 7.27 | 7.44 | 8.87 |
请你通过计算,补全表格
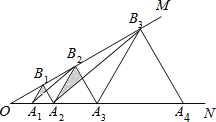
(2)描点、连线:在平面直角坐标系![]() 中,描出表中各组数值所对应的点
中,描出表中各组数值所对应的点![]() ,并画出函数
,并画出函数![]() 关于
关于![]() 的图象:
的图象:

(3)探究性质:随着自变量![]() 的不断增大,函数
的不断增大,函数![]() 的变化趋势:
的变化趋势:
(4)解决问题:当![]() 时,
时,![]() 的长度大约是____
的长度大约是____![]() (保留两位小数).
(保留两位小数).
【答案】(1)![]() (2)详见解析(3)详见解析(4)
(2)详见解析(3)详见解析(4)![]()
【解析】
(1)①当x=BM=0时,当![]() 时,假设
时,假设![]() 交
交![]() 的延长线于点
的延长线于点![]() ,得出
,得出![]() 为
为![]() 的中位线,根据旋转性质
的中位线,根据旋转性质![]() ,即可解答
,即可解答
(2)描点出如下图象,从图象可以看出:随着自变量x的不断增大,函数y的变化趋势;
(3)观察函数图形可知当![]() 时,
时,![]() 随
随![]() 增大而减小,当
增大而减小,当![]() 时,
时,![]() 随
随![]() 增大而增大.
增大而增大.
(4)MN=2BM,设![]() ,得到
,得到![]() ,在证明
,在证明![]() ,得到
,得到![]() ,再利用
,再利用![]() 得到
得到![]() ,代入即可解答
,代入即可解答
(1)当![]() 时,
时,![]() 点与
点与![]() 点分别和
点分别和![]() 点、
点、![]() 点重合,
点重合,![]()
当![]() 时,假设
时,假设![]() 交
交![]() 的延长线于点
的延长线于点![]()
![]()
![]()
又![]() 为
为![]() 的中点
的中点![]()
![]() 为
为![]() 的中位线
的中位线
根据旋转性质
![]()
![]() (外角性质)
(外角性质)
![]()
![]()
![]()
![]()
![]()
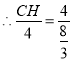
![]() 即
即![]() 点与
点与![]() 点重合
点重合
![]()
(2)根据表格描点可得:
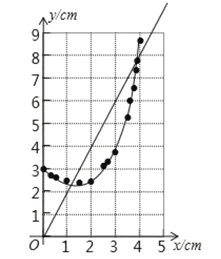
(3)根据图像可得:
当![]() 时,
时,![]() 随
随![]() 增大而减小,
增大而减小,
当![]() 时,
时,![]() 随
随![]() 增大而增大.
增大而增大.
(4)![]()
设![]()
![]()
![]() (外角性质)
(外角性质)
![]()
![]()
![]()
![]()
![]()
![]()
又![]()
![]()
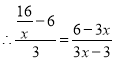
![]()
解得:![]()
所以![]() 的长度大约是4或
的长度大约是4或![]()

练习册系列答案
相关题目