题目内容
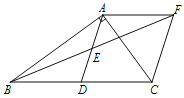
【题目】已知:在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点.过点A做AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;若AC=4,AB=5,求菱形ADCF的面积.
(3)当△ABC满足什么条件时,四边形ADCF是正方形,请说明理由.
【答案】(1)见解析;(2)菱形ADCF的面积=10;(3)当AB=AC时,四边形ADCF是正方形,理由见解析.
【解析】
(1)根据AAS证△AFE≌△DBE;
(2)利用全等三角形的对应边相等得到AF=BD.证出四边形ADCF是平行四边形,再由“直角三角形斜边的中线等于斜边的一半”得到AD=DC,从而得出四边形ADCF是菱形;由直角三角形ABC与菱形有相同的高,根据等积变形求出这个高,代入菱形面积公式可求出结论;
(3)当AB=AC时和D是BC的中点可得:AD⊥BC,从而得出结论.
(1)证明:①∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,AD是BC边上的中线,
∴AE=DE,BD=CD,
在△AEF和△DEB中,
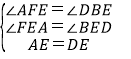 ,
,
∴△AEF≌△DEB(AAS);
(2)证明:由(1)知,△AFE≌△DBE,则AF=DB.
∵DB=DC,
∴AF=CD.
∵AF∥BC,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,E是AD的中点,
∴AD=DC=![]() BC,
BC,
∴四边形ADCF是菱形;
连接DF,如图所示:
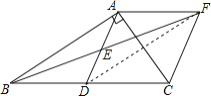
∵AF∥BD,AF=BD,
∴四边形ABDF是平行四边形,
∴DF=AB=5,
∵四边形ADCF是菱形,
∴菱形ADCF的面积=![]() ACDF=
ACDF=![]() ×4×5=10.
×4×5=10.
(3)当AB=AC时,四边形ADCF是正方形,
理由:∵AB=AC,D是BC的中点,
∴ AD⊥BC,
又∵四边形ADCF是菱形,
∴菱形ADCF是正方形.

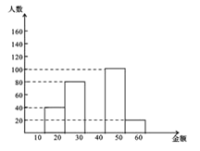
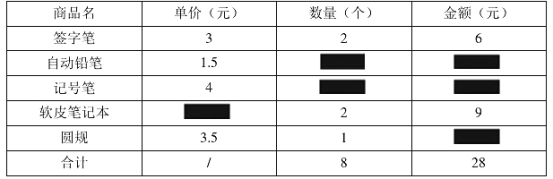
【题目】小明同学为调查某小学六个年级学生每周的零花钱情况,他在学校中随机抽取了400名学生进行调查统计并制成如下图表,
|
|
请根据图表提供的信息解答下列问题:
(1)a =__________,b =__________;
(2)补全频数分布直方图;
(3)若全校共有3000名学生,请你估计该校每周零花钱超过50元的学生有多少名?