题目内容
【题目】如图，直线
分别与x轴、y轴交于
两点，与直线
交于点C（4，2）．
（1）点A坐标为（ ， ），B为（ ， ）；
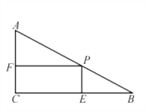
（2）在线段
上有一点E，过点E作y轴的平行线交直线
于点F，设点E的横坐标为m，当m为何值时，四边形
是平行四边形；
（3）若点P为x轴上一点，则在平面直角坐标系中是否存在一点Q，使得
四个点能构成一个菱形．若存在，求出所有符合条件的Q点坐标；若不存在，请说明理由．
【答案】（1）（8，0）；（0，4）．（2）故当
时，四边形
是平行四边形；（3）Q点坐标为
、
、
或
．
【解析】
（1）由点C的坐标利用待定系数法即可求出直线l1的解析式，再分别令直线
的解析式中
求出对应的y、x值，即可得出点A、B的坐标；
（2）由点C的坐标利用待定系数法即可求出直线
的解析式，结合点E的横坐标即可得出点E、F的坐标，再根据平行四边形的性质即可得出关于m的一元一次方程，解方程即可得出结论；
（3）分
为边和为对角线两种情况讨论．当为边时，根据菱形的性质找出点P的坐标，结合A、B的坐标即可得出点Q的坐标；当为对角线时，根据三角形相似找出点P的坐标，再根据菱形对角线互相平分即可得出点Q的坐标．综上即可得出结论．
解：（1）将点C（4，2）代入
中，
得：
，解得：
，
∴直线为
．
令中
，则
，
∴B（0，4）；
令中
，则
，
∴A（8，0）．
（2）∵点C（4，2）是直线
上的点，
∴
，解得：
，
∴直线为
．
∵点E的横坐标为
，
∴
，
∴
．
∵四边形是平行四边形，
∴
，即
，
解得：．
故当时，四边形是平行四边形．
（3）假设存在．
以
为顶点的菱形分两种情况：
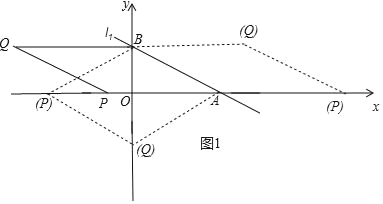
①以为边，如图1所示．
∵点A（8，0），B（0，4），
∴
．
∵以为顶点的四边形为菱形，
∴
或
．
当
时，
或
；
当
时，点P（﹣8，0）．
当时，
，即
；
当P（
）时，
，即
；
当
时，
，即
．
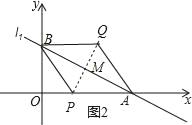
②以为对角线，对角线的交点为M，如图2所示．
∵点
，
∴
．
∵
，
∴
，
∴
，
∴
，
∴
，
∴点
，即（3，0）．
∵以为顶点的四边形为菱形，
∴点
，即（5，4）．
综上可知：若点P为x轴上一点，则在平面直角坐标系中存在一点Q，使得四个点能构成一个菱形，此时Q点坐标为
、、
或
．
