题目内容
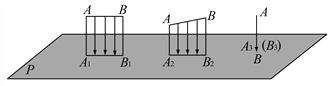
【题目】为解决楼房之间的挡光问题,某地区规定:两幢楼房间的距离至少为40米,中午12时不能挡光.如图,某旧楼的一楼窗台高1米,要在此楼正南方40米处再建一幢新楼.已知该地区冬天中午12时阳光从正南方照射,并且光线与水平线的夹角最小为30°,在不违反规定的情况下,请问新建楼房最高多少米?

【答案】![]() 米
米
【解析】试题分析:在不违反规定的情况下,需使阳光能照到旧楼的一楼窗台;据此构造Rt△DCE,其中有CE=40米,∠DCE=30°,解三角形可得DE的高度,再由DB=BE+ED可计算出新建楼房的最高高度.
试题解析:
解:过点C作CE⊥BD于E.
∵AB=40米,
∴CE=40米,
∵阳光入射角为30°,
∴∠DCE=30°,
在Rt△DCE中tan∠DCE=![]() .
.
∴![]() ,
,
∴DE=40×![]() 米,
米,
∵AC=BE=1米,
∴DB=BE+ED=1+![]() 米.
米.
答:新建楼房最高为![]() 米.
米.


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目