��Ŀ����
����Ŀ���ۺ���̽��
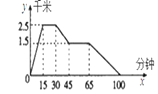
��ͼ1��ƽ��ֱ������ϵ�У�������y=ax2+bx+3��x��ֱ��ڵ�A����2��0����B��4��0������y�ύ�ڵ�C����D��y�Ḻ������һ�㣬ֱ��BD��������y=ax2+bx+3�ڵ��������ڵ�E����4��y����F��������y=ax2+bx+3�ϵ�һ�㣬�ҵ�F��ֱ��BE�Ϸ�������F��ƽ����x���ֱ������ƽ��m����λ���Ⱥ�ǡ������ֱ��BE�ϵĵ�G����
��1����������y=ax2+bx+3�ı���ʽ�������E�����ꣻ
��2�����F�ĺ�����Ϊx����4��x��4��������������⣺
�ٵ���G���D�غ�ʱ����ƽ�ƾ���m��ֵ��
���ú�x��ʽ�ӱ�ʾƽ�ƾ���m������m�����ֵ��
��3����ͼ2������F��x��Ĵ���FP����ֱ��BE�ڵ�P������ΪF������FD���Ƿ���ڵ�F��ʹ��FDP����FDG�������Ϊ1��2�������ڣ�ֱ��д����F�����ꣻ�������ڣ�˵�����ɣ�

���𰸡���1������4����6������2����![]() -1����8����3����������
-1����8����3����������
��������
��1���Ƚ�A����2��0����B��4��0��������y=ax2+bx+3���a��b��ֵ������������ߵı���ʽ���ٽ�E������������ʽ���y��ֵ���ɣ�
��2������ֱ��BD�ı���ʽΪy=kx+b����B��4��0����E����4����6���������k��b��ֵ���ٽ�x=0�������ʽ���D�����꣬����G���D�غ�ʱ���ɵ�G�����꣬GF��x�ᣬ�ʿɵ�F�������꣬ �ٽ�y=��3���������ߵĽ���ʽ���ɵõ�F�����꣬�ٸ���m=FG���ɵ�m��ֵ��
�����F���G�����꣬����m=FG�г����̻���ɵó�m�Ķ��κ�����ϵʽ���ٸ��ݶ��κ�����ͼ��ɵ�m��ȡֵ��Χ��
��3���ֱ��������F��x������ʱ���Ҳ�ʱ�����������������FDP����FDG�������Ϊ1��2����PD��DG=1��2����֪FP��HD����FH��HG=1��2���ٷֱ����F,G������꣬�ٸ��������ϵ�г���ʽ������⼴�ɵ�F������.
�⣺��1����A����2��0����B��4��0��������y=ax2+bx+3�ã�![]() ����ã�
����ã�![]() ��
��
�������ߵı���ʽΪy=��![]() x2+
x2+![]() x+3��
x+3��
��E����4��y������ã�y=��6��
���E����������4����6����
��2������ֱ��BD�ı���ʽΪy=kx+b����B��4��0����E����4����6������ã�![]() ��
��
��ã�![]() ��
��
��ֱ��BD�ı���ʽΪy=![]() x��3��
x��3��
��x=0����y=![]() x��3�ã�y=��3��
x��3�ã�y=��3��
��D��0����3����
����G���D�غ�ʱ��G������Ϊ��0����3����
��GF��x�ᣬ
��F����������3��
��y=��3���������ߵĽ���ʽ�ã���![]() x2+
x2+![]() x+3=��3��
x+3=��3��
��ã�x=![]() +1��x=��
+1��x=��![]() +1��
+1��
����4��x��4��
���F����������![]() +1����3����
+1����3����
��m=FG=![]() ��1��
��1��
�����F��������x����![]() x2+
x2+![]() x+3�������G��������x+m��
x+3�������G��������x+m��![]() ��x+m����3����
��x+m����3����
����![]() x2+
x2+![]() x+3=
x+3=![]() ��x+m����3������ã�m=��
��x+m����3������ã�m=��![]() x2+8��
x2+8��
����![]() ��0��
��0��
��m�����ֵ��
��x=0ʱ��m�����ֵΪ8��
��3������F��x������ʱ������ͼ��ʾ��
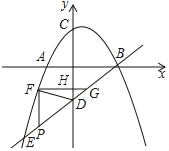
�ߡ�FDP����FDG�������Ϊ1��2��
��PD��DG=1��2��
��FP��HD��
��FH��HG=1��2��
��F��������x����![]() x2+
x2+![]() x+3�������G����������2x����
x+3�������G����������2x����![]() x��3����
x��3����
����![]() x2+
x2+![]() x+3=��
x+3=��![]() x��3�������ã�x2��6x��16=0��
x��3�������ã�x2��6x��16=0��
��ã�x=��2��x=8����ȥ����
���F����������2��0����
����F��x����Ҳ�ʱ������ͼ��ʾ��
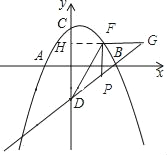
�ߡ�FDP����FDG�������Ϊ1��2��
��PD��DG=1��1��
��FP��HD��
��FH��HG=1��1��
��F��������x����![]() x2+
x2+![]() x+3�������G��������2x��
x+3�������G��������2x��![]() x��3����
x��3����
����![]() x2+
x2+![]() x+3=
x+3=![]() x��3�������ã�x2+2x��16=0��
x��3�������ã�x2+2x��16=0��
��ã�x=![]() ��1��x=��
��1��x=��![]() ��1����ȥ����
��1����ȥ����
���F��������![]() ��1��
��1��![]() ����
����
������������F����������2��0����![]() ��1��
��1��![]() ����
����

����Ŀ�����κ���y��ax2��bx��c(a��b��cΪ��������a��0)�е�x��y�IJ��ֶ�Ӧֵ���±���
x | ��1 | 0 | 1 | 3 |
y | ��1 | 3 | 5 | 3 |
���н��ۣ���c��3���ڵ�x��1ʱ��y��ֵ��x���������С���ۺ��������ֵ��5����abc��0.������ȷ����(����)
A. 4�� B. 3�� C. 2�� D. 1��