题目内容
【题目】如图,△ABC与△ABD都是等边三角形,点E,F分别在BC,AC上,BE=CF,AE与BF交于点G.

(1)求∠AGF的度数;
(2)连接DG,若AG=3、BG=2,求DG的长.
【答案】(1)∠AGF=60°;(2)DG=5.
【解析】
(1)根据等边三角形的性质得到AB=BC,∠ABC=∠C=60°,再根据三角形全等的判定方法可证得△ABE≌△BCF,则∠BAE=∠FBC,利用三角形外角性质得∠BGE=∠ABG+∠BAE,则∠BGE=∠ABG+∠FBC=∠ABC=60°,然后根据对顶角相等即可得到结论;
(2)延长GE至点H,使GH=GB,由于∠BGE=60°,根据等边三角形的判定得到△BGH为等边三角形,然后根据等边三角形的性质得到BG=BH=GH,∠GBH=60°,且AB=BD,∠ABD=60°,易得∠ABH=∠DBG,根据三角形全等的判定方法可证得△DBG≌△ABH(SAS),则DG=AH,即可得到DG=AG+BG.
(1)解:∵△ABC是等边三角形,
∴AB=BC,∠ABC=∠C=60°,
∵在△ABE和△BCF中,
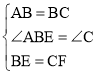 ,
,
∴△ABE≌△BCF(SAS),
∴∠BAE=∠FBC,
∵∠BGE=∠ABG+∠BAE=∠ABG+∠FBC=∠ABC=60°,
∴∠AGF=∠BGE=60°;
(2)证明:延长GE至点H,使GH=GB,如图,
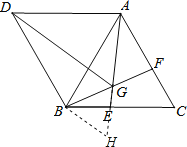
∵∠BGE=60°,
∴△BGH为等边三角形,
∴BG=BH=GH,∠GBH=60°,
∵△ABD是等边三角形,
∴AB=BD,∠ABD=60°,
∵∠ABH=∠GBH+∠ABG,∠DBG=∠ABD+∠ABG,
∴∠ABH=∠DBG,
∵在△DBG和△ABH中,
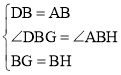 ,
,
∴△DBG≌△ABH(SAS),
∴DG=AH,
而AH=AG+GH,
∴DG=AG+BG,
∵AG=3,BG=2,
∴DG=5.







