题目内容
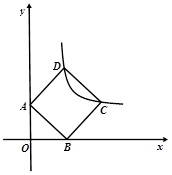
 如图,如图正方形ABCD内一点E,满足△CDE为正三角形,直线AE交BC于F点,过E点的直线GH⊥AF,交AB于点G,交CD于点H.以下结论:
如图,如图正方形ABCD内一点E,满足△CDE为正三角形,直线AE交BC于F点,过E点的直线GH⊥AF,交AB于点G,交CD于点H.以下结论:①∠AFC=105°;②GH=2EF;③
| 2 |
| AE |
| EH |
| 2 |
| 3 |
其中正确的有( )
分析:根据等边三角形的性质求出∠CDE,然后求出∠ADE=30°,再根据等腰三角形的性质求出∠DAE=75°,然后求出∠BAF=15°,根据三角形的一个外角等于与它不相邻的两个内角的和求出∠AFC=105°,判断出①正确,过点H作HK⊥AB,可得HK=AD,根据等角的余角相等求出∠BAF=∠KHG,再利用“角角边”证明△ABF和△HKG,然后根据全等三角形对应边相等可得AF=GH,再根据等边三角形的性质,点E是AF的中点,从而得到GH=2EF,判断出②正确;再求出∠CEF=∠CEH=45°,过点F作FM⊥CE于M,过点H作HN⊥CE于N,解直角三角形分别用MF、CN表示出CE,可以得到MF=CN,再表示出CE,即可判定③正确;设MF=CN=x,表示出EF、EH,然后求出
的值,判断出④错误.
| AE |
| EH |
解答:解:∵△CDE为正三角形,
∴∠CDE=60°,
∴∠ADE=90°-60°=30°,
∵AD=DE=CD,
∴∠DAE=∠DEA=
(180°-30°)=75°,
∴∠BAF=90°-75°=15°,
∴∠AFC=90°+15°=105°,故①正确;
过点H作HK⊥AB,则HK=AD,
∵GH⊥AF,
∴∠BAF+∠AGE=90°,
又∵∠AGE+∠KHG=90°,
∴∠BAF=∠KHG,
在△ABF和△HKG中,
,
∴△ABF≌△HKG(AAS),
∴AF=GH,
∵△CDE为正三角形,
∴点E在CD的垂直平分线上,
根据平行线分线段成比例定理,点E是AF的中点,
∴AF=2EF,
∴GH=2EF,故②正确;
∵GH⊥AF,∠DEA=75°,
∴∠DEH=90°-75°=15°,
∴∠CEH=60°-15°=45°,
∴∠CEF=90°-45°=45°,
过点F作FM⊥CE于M,过点H作HN⊥CE于N,
则MF=EM,NH=EN,
∵△CDE是等边三角形,
∴∠DCE=60°,
∴∠ECF=90°-60°=30°,
∴CM=
MF,NH=
CN,
∴CE=
MF+MF=
CN+CN,
∴MF=CN,
∴CE=
EF+
EH,
∴
CE=EF+EH,故③正确;
=
=
=
,故④错误.
综上所述,正确的结论是①②③.
故选A.
∴∠CDE=60°,
∴∠ADE=90°-60°=30°,
∵AD=DE=CD,
∴∠DAE=∠DEA=
| 1 |
| 2 |
∴∠BAF=90°-75°=15°,
∴∠AFC=90°+15°=105°,故①正确;
过点H作HK⊥AB,则HK=AD,
∵GH⊥AF,
∴∠BAF+∠AGE=90°,
又∵∠AGE+∠KHG=90°,
∴∠BAF=∠KHG,
在△ABF和△HKG中,
|

∴△ABF≌△HKG(AAS),
∴AF=GH,
∵△CDE为正三角形,
∴点E在CD的垂直平分线上,
根据平行线分线段成比例定理,点E是AF的中点,
∴AF=2EF,
∴GH=2EF,故②正确;
∵GH⊥AF,∠DEA=75°,
∴∠DEH=90°-75°=15°,
∴∠CEH=60°-15°=45°,
∴∠CEF=90°-45°=45°,
过点F作FM⊥CE于M,过点H作HN⊥CE于N,
则MF=EM,NH=EN,
∵△CDE是等边三角形,
∴∠DCE=60°,
∴∠ECF=90°-60°=30°,
∴CM=
| 3 |
| 3 |
∴CE=
| 3 |
| 3 |
∴MF=CN,
∴CE=
| ||
| 2 |
| ||
| 2 |
∴
| 2 |
| AE |
| EH |
| EF |
| EH |
| ||||
|
| ||
| 3 |
综上所述,正确的结论是①②③.
故选A.
点评:本题考查了四边形综合题型,主要利用了正方形的性质,等边三角形的性质,全等三角形的判断与性质,解直角三角形,等腰直角三角形的判定与性质,作辅助线构造出全等三角形与等腰直角三角形是解题的关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
 答案直接填写在后面的横线上
答案直接填写在后面的横线上
 轴、
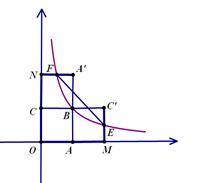
轴、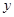 轴上,四边形OABC是面积为4的正方形,函数
轴上,四边形OABC是面积为4的正方形,函数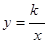 (
(
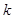 = ;
= ;
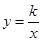 (
(