题目内容
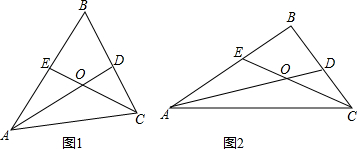
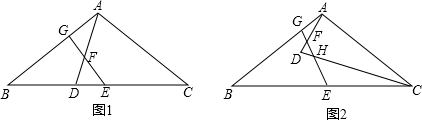
如图1,在△ABC中,AB=AC,CD⊥BA交BA的延长线于点D.一正方形EFGH的一条边EH与AC边在一条直线上,另一条边EF恰好经过点B.(1)在图1中,请你通过观察、测量BE与CD的长度,猜想并写出BE与CD满足的数量关系,然后证明你的猜想;
(2)将正方形EFGH沿AC方向平移到图2所示的位置时,EH边仍与AC边在同一直线上,另一条边EF交BC边于点M,过点M作MN⊥BA于点N.此时请你通过观察、测量ME、MN与CD的长度,猜想并写出ME、MN与CD之间满足的数量关系,然后证明你的猜想;
(3)将正方形EFGH沿CA方向平移到图3所示的位置时,EH边仍与AC边在同一直线上,另一条边EF的延长线交CB边的延长线于点M,过点M作MN⊥AB交AB的延长线于点N.此时请你猜想并写出ME、MN与CD之间满足的数量关系,不需证明.
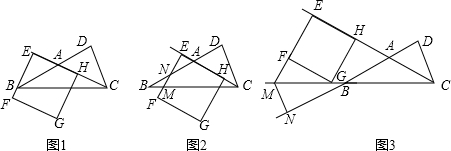
分析:(1)根据全等三角形的判定定理ASA推知△BEC≌△CDB,然后由全等三角形的对应边相等证得BE=CD;
(2)作辅助线MK⊥CD于K构建矩形MNDK,然后理由矩形的对边平行且相等、平行线的性质、已知条件AB=AC来证明△EMC≌△KCM(AAS);最后利用全等三角形的性质推知ME=CK,所以CK+KD=ME+MN=CD,即ME+MN=CD;
(3)作辅助线“过C作CK⊥MN于K”构建矩形CKND.然后利用矩形CNKD、正方形EFGH的性质以及已知条件AB=AC推知△ECM≌△KCM,由全等三角形的对应边相等知EM=KM,所以根据MK=MN+NK推知ME-MN=CD.
(2)作辅助线MK⊥CD于K构建矩形MNDK,然后理由矩形的对边平行且相等、平行线的性质、已知条件AB=AC来证明△EMC≌△KCM(AAS);最后利用全等三角形的性质推知ME=CK,所以CK+KD=ME+MN=CD,即ME+MN=CD;
(3)作辅助线“过C作CK⊥MN于K”构建矩形CKND.然后利用矩形CNKD、正方形EFGH的性质以及已知条件AB=AC推知△ECM≌△KCM,由全等三角形的对应边相等知EM=KM,所以根据MK=MN+NK推知ME-MN=CD.
解答:解:(1)BE=CD…2分
证明:∵在△ABC中,AB=AC,
∴∠ABC=∠ACB(等边对等角);
又∵CD⊥BA,BE⊥CE,
∴∠EBC=∠DCB(等角的余角相等);
在△BEC和△CDB中,
,
∴△BEC≌△CDB(ASA),
∴BE=CD(全等三角形的对应边相等);
(2)ME+MN=CD.…3分
证明:作MK⊥CD于K.
∵MN⊥BA于N,∠D=90°,MK⊥CD,
∴四边形MNDK为矩形.
∴MN=KD,MK∥BD.…4分
∴∠DBC=∠KMC.
∵AB=AC,
∴∠ECM=∠DBC=∠KMC.…5分
又∵∠E=∠MKC=90°,CM=MC,
∴△EMC≌△KCM(AAS).
∴ME=CK.…6分
∴CK+KD=ME+MN=CD,即ME+MN=CD.…7分
(3)ME-MN=CD.…8分
过C作CK⊥MN于K.
∵MN⊥BA,CD⊥BA,
∴四边形CKND是矩形.…9分
∴CD=NK,CK∥BA.
∴∠MCK=∠DBC.
又∵AC=AB,
∴∠DCB=∠BCA.
又∵∠ECM=∠BCA,
∴∠ECM=∠MCK.
∵正方形EFGH,
∴∠HEF=∠MEC=90°.
又∵MC=MC,
∴△ECM≌△KCM.
∴EM=KM.…11分
又∵MK=MN+NK,
∴ME-MN=CD.…12分
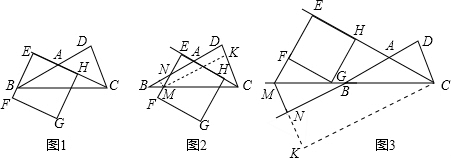
证明:∵在△ABC中,AB=AC,
∴∠ABC=∠ACB(等边对等角);
又∵CD⊥BA,BE⊥CE,
∴∠EBC=∠DCB(等角的余角相等);
在△BEC和△CDB中,
|
∴△BEC≌△CDB(ASA),
∴BE=CD(全等三角形的对应边相等);
(2)ME+MN=CD.…3分
证明:作MK⊥CD于K.
∵MN⊥BA于N,∠D=90°,MK⊥CD,
∴四边形MNDK为矩形.
∴MN=KD,MK∥BD.…4分
∴∠DBC=∠KMC.
∵AB=AC,
∴∠ECM=∠DBC=∠KMC.…5分
又∵∠E=∠MKC=90°,CM=MC,
∴△EMC≌△KCM(AAS).
∴ME=CK.…6分
∴CK+KD=ME+MN=CD,即ME+MN=CD.…7分
(3)ME-MN=CD.…8分
过C作CK⊥MN于K.
∵MN⊥BA,CD⊥BA,
∴四边形CKND是矩形.…9分
∴CD=NK,CK∥BA.
∴∠MCK=∠DBC.
又∵AC=AB,
∴∠DCB=∠BCA.
又∵∠ECM=∠BCA,
∴∠ECM=∠MCK.
∵正方形EFGH,
∴∠HEF=∠MEC=90°.
又∵MC=MC,
∴△ECM≌△KCM.
∴EM=KM.…11分
又∵MK=MN+NK,
∴ME-MN=CD.…12分

点评:本题综合考查了全等三角形的判定与性质、等腰三角形的性质、正方形的性质.在证明(2)、(3)的结论时,都是通过作辅助线构建矩形来推理三角形全等的.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 明理由.
明理由.
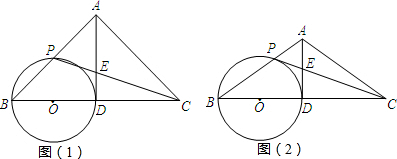
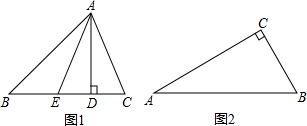 如图1,AD和AE分别是△ABC的BC边上的高和中线,点D是垂足,点E是BC的中点,规定:λA=
如图1,AD和AE分别是△ABC的BC边上的高和中线,点D是垂足,点E是BC的中点,规定:λA=