题目内容
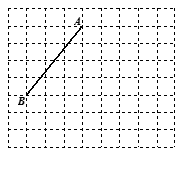
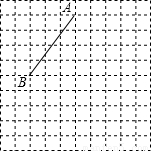
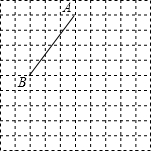
如图线段AB的端点在边长为1的正方形网格的格点上，现将线段AB绕点A按逆时针方向旋转90°得到线段AC．（1）请你在所给的网格中画出线段AC；
（2）判断将线段AB旋转到线段AC的过程中，线段AB扫过的区域所形成的图形是哪个立体图形的侧面展开图？将
答案直接填写在后面的横线上（3）求出（2）中所说立体图形的侧面展开图的面积．
分析：（1）作CA⊥AB，且AC=AB．
（2）由于以点A为圆心逆时针方向旋转90°，得到的是扇形，而圆锥的侧面展开图是扇形．
（3）根据勾股定理，由网格中可得，AB=5，∠BAC=90°，由扇形面积公式S=
求得扇形的面积．
（2）由于以点A为圆心逆时针方向旋转90°，得到的是扇形，而圆锥的侧面展开图是扇形．
（3）根据勾股定理，由网格中可得，AB=5，∠BAC=90°，由扇形面积公式S=
| nπR2 |
| 360 |
解答：解：（1）如图．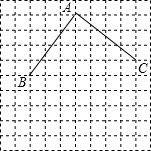
（2）圆锥．
（3）由勾股定理得，AB=
=5．由于侧面展开图，∠BAC=90°，
∴由扇形面积公式S=
得，S=
=
．
（2）圆锥．
（3）由勾股定理得，AB=
| 32+42 |
∴由扇形面积公式S=
| nπR2 |
| 360 |
| 90π×52 |
| 360 |
| 25π |
| 4 |
点评：本题利用了勾股定理和扇形面积公式求解．
练习册系列答案
阅读快车系列答案
相关题目
转90°得到线段AC．
