Question

【题目】问题探究

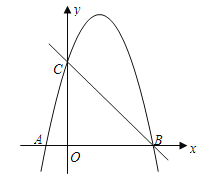
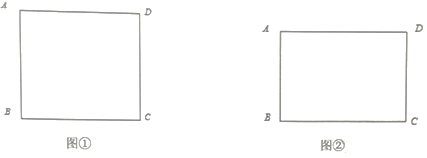
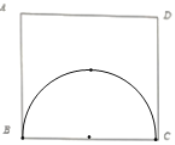
（1）如图①，在正方形ABCD内，请画出使∠BPC=90°的所有点P；

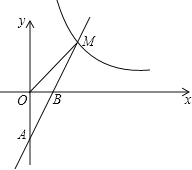
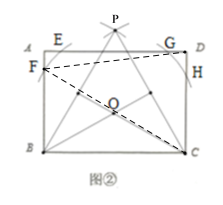
（2）如图②，已知矩形ABCD，AB=9，BC=10，在矩形ABCD内(含边)画出使∠BPC=60°的所有点P，并求出△APD面积的最大值；

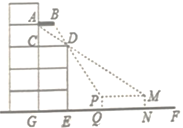
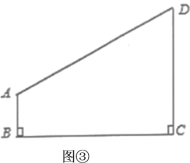
（3）随着社会发展，农业观光园走进了我们的生活，某农业观光园的平面示意图如图3所示的四边形ABCD，其中∠A=120°，∠B=∠C=90°，AB=km，BC=6km，观光园的设计者想在园中找一点P，使得点P与点A、B、C、D所连接的线段将整个观光园分成四个区域，用来进行不同的设计与规划，从实用和美观的角度他们还要求在△BPC的区域内∠BPC=120°，且△APD的区域面积最小，试问在四边形ABCD内是否存在这样的点P，使得∠BPC=120°，且△APD面积最小？若存在，请你在图中画出点P点的位置，并求出△APD的最小面积.若不存在，说明理由.

Answer 1

【答案】（1）见解析；（2）45-；（3）9-12.

【解析】

（1）如图，以BC为直径作上半圆（不含点B、C），根据直径所对的圆周角为直角得到该半圆上的任意一点即可；（2）以BC为边作等边△BPC；作等边△BPC的外接圆⊙O与AB交于F，与AD交于点E、G，与CD交于点H，和即为所求，（3）以BC为边向下作等边△BCQ，作△BCQ的外接圆⊙O，则劣弧BC即为所求，作AD的平行线MN切劣弧BC于P，连接OP并延长交AD于E，由切线的性质可得OP⊥MN，即可证明OP⊥AD，由平行线间垂线段最短，可得三角形APD面积最小，过A作AH⊥CD于H，由BC=10可得△BCQ的外接圆半径为2，与BC弦的弦心距为，根据AB=可得AH与⊙O相切，切点为G，根据平行线的判定定理可得OC//AD，进而可证明四边形OCDF为平行四边形，即可证明CD=OF，根据直角三角形锐角互余的关系可得∠EOF=30°，通过解直角三角形可求出OE的长，进而可求出PE的长，根据三角形面积公式即可得答案.

（1）如图，以BC为直径作上半圆（不含点B、C），

∵直径所对的圆周角是90°，

∴（不含点B、C）即为所求.

（2）以BC为边作等边△BPC；作等边△BPC的外接圆⊙O与AB交于F，与AD交于点E、G，与CD交于点H，

∵△BPC是等边三角形，和是弦BC所对圆周角，

∴和即为所求.

连接CF，DF，

∵三角形的底相等，高越大面积越大，

∴当P点与F点或H点重合时面积最大，

∵∠BFC=60°，BC=10，

∴tan60°===，

∴BF=，

∴AF=9-，

∴S△AFD=×（9-）×10=45-.

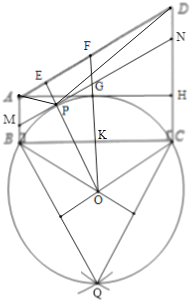
（3）如图，以BC为边向下作等边△BCQ，作△BCQ的外接圆⊙O，则劣弧BC即为所求，作AD的平行线MN切劣弧BC于P，连接OP并延长交AD于E，

∴OP⊥MN，

∵AD//MN，

∴OE⊥AD，

∵平行线间垂线段最短，

∴△APD面积最小，

过A作AH⊥CD于H，作OK⊥BC，延长OK交AH于G，交AD于F，

∵△BCQ是等边三角形，

∴∠OBC=30°，BK=3，

∴OB==，OK==，即外接圆的半径为，BC的弦心距为，

∵∠DCB=90°，

∴AH//BC，

∴OG⊥AH，

∴AB=KG=CH，

∵AB=，

∴OG=OK+KG=OK+AB=2=OB，

∴AH与⊙O相切，切点为G，

∵∠D=60°，∠OCD=90°+30°=120°，

∴AD//OC，

∵∠OKC=∠DCK=90°，

∴OF//CD，

∴四边形OCDF是平行四边形，

∴OF=CD，

∵∠BAD=120°，∠BAH=90°，

∴∠FAG=30°，

∵∠FAG+∠AFO=90°，∠EOF+∠AFO=90°，

∴∠EOF=∠FAG=30°，

∵∠FAG=30°，AH=BC=6，

∴AD==，HD=6tan30°=2，

∴OF=CD=HD+CH=2+=3，

∴OE=OFcos∠EOF=OFcos30°=3×=，

∴PE=OE-OP=-2，

∴S△APD=ADPE=×（-2）×=9-12.