��Ŀ����
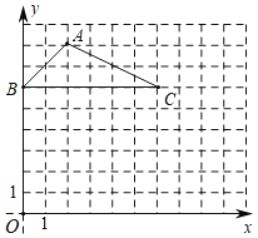
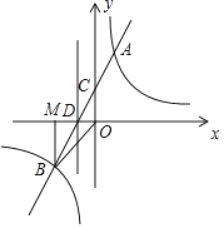
����Ŀ����ͼ��һ�κ���y��mx+n��m��0����ͼ���뷴��������y��![]() ��k��0����ͼ���ڵ�һ���������ڵ�A��B���㣬��y�ύ�ڵ�C������B��BM��x�ᣬ����Ϊ��M��BM��OM��2����A��������Ϊ4��
��k��0����ͼ���ڵ�һ���������ڵ�A��B���㣬��y�ύ�ڵ�C������B��BM��x�ᣬ����Ϊ��M��BM��OM��2����A��������Ϊ4��
��1����÷�����������һ�κ����ı���ʽ��
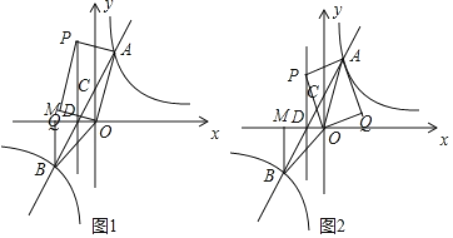
��2��ֱ��AB��x���ڵ�D������D��ֱ��l��x�ᣬ���ֱ��l�ϴ��ڵ�P������ƽ���ڴ��ڵ�Q��ʹ�ı���OPAQ�Ǿ��Σ������P�����꣮
���𰸡���1��y��![]() ��y��2x+2����2�����ڣ�����1��
��y��2x+2����2�����ڣ�����1��![]() ����1��2+
����1��2+![]() ����1��2��
����1��2��![]() ����
����
��������
��1����������ó�B�����꣬�����ó���������������ʽ�������ô���ϵ�����ó�һ�κ�������ʽ��
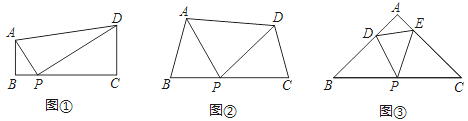
��2����P��-1��a������ͼ1������PAO=90������ͼ2������APO=90�������ݹ��ɶ����з��̼��ɵõ����ۣ�
�⣺��1����BM��OM��2��
���B����������2����2����
�跴���������Ľ���ʽΪy��![]() ��
��
��2��![]() ��
��
��k��4��
�෴���������Ľ���ʽΪy��![]() ��
��
�ߵ�A����������4��
��4��![]() ��
��
��x��1��
���A��������1��4����
��һ�κ���y��mx+n��m��0����ͼ�����A��1��4������B����2����2����
��![]() ��
��
��ã�![]() ��
��
��һ�κ����Ľ���ʽΪy��2x+2��
��2�����ڣ�
��ֱ��AB��x�ύ��D��
��D����1��0����
��OD��1��
��P����1��a����
��ͼ1������PAO��90����
��OP2��PA2+OA2��PD2+OD2��
�ࣨ1+1��2+��4��a��2+12+42��12+a2��
��ã�a��![]() ��
��
��P����1��![]() ����
����
��ͼ2������APO��90����
��OP2��OA2��PA2��PD2+OD2��
��12+42��[��1+1��2+��4��a��2]��12+a2��
��ã�a��2��![]() ��
��
��P����1��2+![]() ����1��2��
����1��2��![]() ����
����
������������P����������1��![]() ����1��2+
����1��2+![]() ����1��2��
����1��2��![]() ����
����
�ʴ�Ϊ����1��y��![]() ��y��2x+2����2�����ڣ�����1��
��y��2x+2����2�����ڣ�����1��![]() ����1��2+
����1��2+![]() ����1��2��
����1��2��![]() ����
����