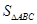题目内容
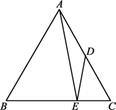
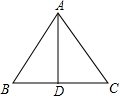 如图,在正△ABC中,D为BC中点,则∠BAD的度数为
如图,在正△ABC中,D为BC中点,则∠BAD的度数为
- A.30°
- B.60°
- C.50°
- D.45°
A
分析:由等边三角形的性质可知∠BAC=60°,再由D为BC中点可知AD是∠BAC的平分线,由角平分线的定义即可得出结论.
解答:∵△ABC是等边三角形,
∴∠BAC=60°,
∵D为BC的中点,
∴AD是∠BAC的平分线,
∴∠BAD= ∠BAC=
∠BAC= ×60°=30°.
×60°=30°.
故选A.
点评:本题考查的是等边三角形的性质,熟知等边三角形三线合一的性质是解答此题的关键.
分析:由等边三角形的性质可知∠BAC=60°,再由D为BC中点可知AD是∠BAC的平分线,由角平分线的定义即可得出结论.
解答:∵△ABC是等边三角形,
∴∠BAC=60°,
∵D为BC的中点,
∴AD是∠BAC的平分线,
∴∠BAD=
 ∠BAC=
∠BAC= ×60°=30°.
×60°=30°.故选A.
点评:本题考查的是等边三角形的性质,熟知等边三角形三线合一的性质是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
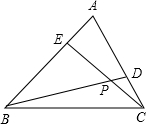 如图,在正△ABC中,D为AC上一点,E为AB上一点,BD,CE交于P,若四边形ADPE与△BPC面积相等,则∠BPE的度数为( )
如图,在正△ABC中,D为AC上一点,E为AB上一点,BD,CE交于P,若四边形ADPE与△BPC面积相等,则∠BPE的度数为( )| A、60° | B、45° | C、75° | D、50° |
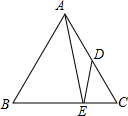 如图,在正△ABC中,点D是AC的中点,点E在BC上,且
如图,在正△ABC中,点D是AC的中点,点E在BC上,且
 如图,在正△ABC中,D为BC中点,则∠BAD的度数为( )
如图,在正△ABC中,D为BC中点,则∠BAD的度数为( ) =
= .
.
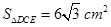 ,求
,求