题目内容
如图,在正△ABC中,点D是AC的中点,点E在BC上,且 =
= .
.
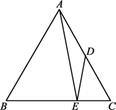
求证:(1)△ABE∽△DCE;
(2)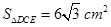 ,求
,求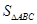
【答案】
(1)∵ΔABC是正三角形
∴∠B=∠C,AB=AC
∵点D是AC的中点
∴AC=2CD
∵ =
=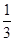
∴BE=2CE
∴ =
=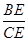
∵∠B=∠C
∴ΔABE∽ΔDCE;
(2)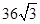
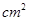
【解析】
试题分析:(1)由ΔABC是正三角形可得∠B=∠C,AB=AC,再结合点D是AC的中点, =
=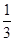 ,即可证得结论;
,即可证得结论;
(2)由(1)知△ABE∽△DCE,由相似三角形的性质可得△ABE的面积,即可求得△AED与△EDC的面积,从而得到结果.
(1)∵ΔABC是正三角形
∴∠B=∠C,AB=AC
∵点D是AC的中点
∴AC=2CD
∵ =
=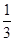
∴BE=2CE
∵∠B=∠C
∴ =
=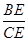
∴ΔABE∽ΔDCE;
(2)∵△ABE∽△DCE
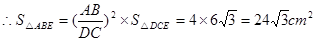
又∵AD=DC且△AED与△EDC具有相同的高和底


考点:本题主要考查相似三角形的判定与性质
点评:解答本题的关键是已知其中一个三角形的面积,根据两个相似三角形的面积之比等于边之比的平方,求出另一个三角形的面积,另外熟记同底同高的三角形的面积相等.

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
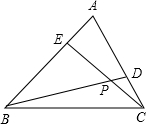 如图,在正△ABC中,D为AC上一点,E为AB上一点,BD,CE交于P,若四边形ADPE与△BPC面积相等,则∠BPE的度数为( )
如图,在正△ABC中,D为AC上一点,E为AB上一点,BD,CE交于P,若四边形ADPE与△BPC面积相等,则∠BPE的度数为( )| A、60° | B、45° | C、75° | D、50° |
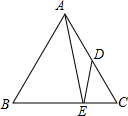 如图,在正△ABC中,点D是AC的中点,点E在BC上,且
如图,在正△ABC中,点D是AC的中点,点E在BC上,且
 如图,在正△ABC中,D为BC中点,则∠BAD的度数为( )
如图,在正△ABC中,D为BC中点,则∠BAD的度数为( )