题目内容
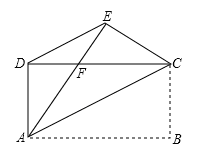
如图,已知四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,连接DE.若DE:AC=3:5,则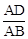 的值为
的值为
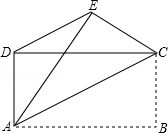
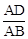 的值为
的值为
A. | B. | C. | D. |
A。
∵矩形沿直线AC折叠,点B落在点E处,
∴∠BAC=∠EAC,AE=AB=CD。
∵矩形ABCD的对边AB∥CD,∴∠DAC=∠BAC
∴∠EAC=∠DAC。
设AE与CD相交于F,则AF=CF。
∴AE-AF=CD-CF,即DF=EF。∴ 。
。
又∵∠AFC=∠EFD,∴△ACF∽△EDF,∴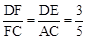 。
。
∴设DF=3x,FC=5x,则AF=5x。
在Rt△ADF中, 。
。
又∵AB=CD=DF+FC=3x+5x=8x,∴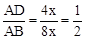 。故选A。
。故选A。
∴∠BAC=∠EAC,AE=AB=CD。
∵矩形ABCD的对边AB∥CD,∴∠DAC=∠BAC
∴∠EAC=∠DAC。
设AE与CD相交于F,则AF=CF。
∴AE-AF=CD-CF,即DF=EF。∴
 。
。又∵∠AFC=∠EFD,∴△ACF∽△EDF,∴
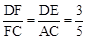 。
。∴设DF=3x,FC=5x,则AF=5x。
在Rt△ADF中,
 。
。又∵AB=CD=DF+FC=3x+5x=8x,∴
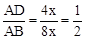 。故选A。
。故选A。

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目


 角
角 角
角 角
角 角
角 ,则AP的长为_____.
,则AP的长为_____.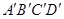 ,他们的面积之比为36∶25,若四边形
,他们的面积之比为36∶25,若四边形


 ABCD的两条对角线AC、BD相交于点
ABCD的两条对角线AC、BD相交于点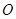 ,
,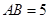 ,
,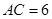 ,
,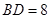 ,则
,则
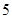 B.
B.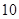 C.
C. D.
D.