题目内容
【题目】如图，已知抛物线y＝－x2＋bx＋c与x轴交于A、B(3，0)两点，与y轴交于点C(0，3)．
(1)求抛物线的解析式及顶点M的坐标；
(2)在抛物线的对称轴上找到点P，使得△PAC的周长最小，并求出点P的坐标．
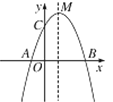
【答案】（1）M为（1，4）．
（2）P（1，2）．
【解析】
（1）利用B、C两点坐标求出抛物线的解析式，根据抛物线的性质得出M点坐标；
（2）根据A、B关于抛物线的对称轴对称得出AP=BP,那么△PAC的周长最小就是CPB在一条直线上，从而求出P点坐标。
（1）∵ 抛物线y = －x2+bx+c 过B（3，0）C（0，3）两点，
∴c=3, －9+3b+3=0，解得b=2 ．
∴ 抛物线的解析式为
，
顶点M为（1，4）．
（2）∵ 点A、B关于抛物线的对称轴对称，
∴ 连结BC与抛物线对称轴交于一点，即为所求点P
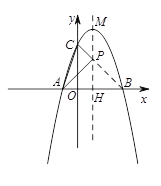
设对称轴与x轴交于点H，
∵ PH∥y轴，
∴ △PHB∽△CBO．
∴
．
由题意得BH=2，CO=3，BO=3，
∴ PH=2．
∴ P（1，2）．
练习册系列答案
考前必练系列答案
相关题目
【题目】某商场用2500元购进A、B两种新型节能台灯共50盏，这两种台灯的进价、标价如下表所示．
类型 价格 | A型 | B型 |
进价（元/盏） | 40 | 65 |
标价（元/盏） | 60 | 100 |
（1）这两种台灯各购进多少盏？
（2）在每种台灯销售利润不变的情况下，若该商场计划销售这批台灯的总利润至少为1400元，问至少需购进B种台灯多少盏？
