题目内容
【题目】如图所示,已知点N(1,0),直线y=﹣x+2与两坐标轴分别交于A,B两点,M,P分别是线段OB,AB上的动点,则PM+MN的最小值是 . 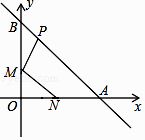
【答案】![]()
【解析】解:如图,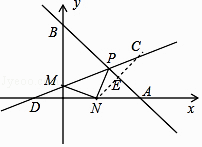
点N关于OB的对称点D(﹣1,0),点N关于直线AB的对称点C,
∵直线AB的解析式为y=﹣x+2,
∴直线NC的解析式为y=x﹣1,
由 ![]() 解得
解得 ![]() ,
,
∴E( ![]() ,
, ![]() ),
),
∵E是NC中点,
∴可得C(4,1).
连接DC与BO交于点M,与AB交于点P,此时PM+MN最小,
∴直线CD的解析式为:y= ![]() x+
x+ ![]() ,
,
由 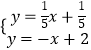 解得:
解得: ![]() ,
,
∴P( ![]() ,
, ![]() ),
),
∴PM+MN=PD= ![]() =
= ![]() .
.
∴PM+MN的最小值是 ![]() ,
,
所以答案是 ![]() .
.
【考点精析】关于本题考查的一次函数的性质,需要了解一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小才能得出正确答案.

练习册系列答案
相关题目
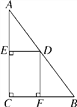
【题目】如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处;
(1)求证:B′E=BF;
(2)设AE=a,AB=b,BF=C,试猜想a,b,c之间的一种关系,并给予证明.

【题目】如图,某计算装置有一數据输入口A和一运算结果的输出口B,表格中是小明输入的一些数据和这些数据经该装置计算后输出的相应结果,按照这个计算装置的计算规律,若输入的数是10,则输出的数是( )
A | 1 | 2 | 3 | 4 | 5 |
B | 0 | 3 | 8 | 15 | 24 |
A. 99 B. 100 C. 101 D. 102