题目内容
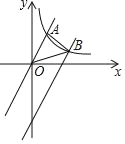
【题目】如图1,已知直角梯形ABCO中,∠AOC=90°,AB∥x轴,AB=6,若以O为原点,OA,OC所在直线为y轴和x轴建立如图所示直角坐标系,A(0,a),C(c,0)中a,c满足|a+c﹣10|+![]() =0
=0
(1)求出点A、B、C的坐标;
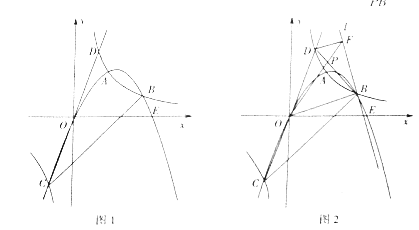
(2)如图2,若点M从点C出发,以2单位/秒的速度沿CO方向移动,点N从原点出发,以1单位/秒的速度沿OA方向移动,设M、N两点同时出发,且运动时间为t秒,当点N从点O运动到点A时,点M同时也停止运动,在它们的移动过程中,当2S△ABN≤S△BCM时,求t的取值范围:
(3)如图3,若点N是线段OA延长上的一动点,∠NCH=k∠OCH,∠CNQ=k∠BNQ,其中k>1,NQ∥CJ,求![]() 的值(结果用含k的式子表示).
的值(结果用含k的式子表示).

【答案】(1)A(0,3),B(6,3), C(7,0);(2)t的取值范围为2≤t≤3;(3)![]()
【解析】
(1)由绝对值和算术平方根的非负性质得出a+c﹣10=0,且c﹣7=0,求出c=7,a+c=10,得出c=3,即可得出答案;
(2)由题意得ON=t,CM=2t,得出AN=3﹣t,由2S△ABN≤S△BCM和三角形面积公式得出不等式,解得t≥2,由0≤t≤3,即可得出答案;
(3)设AB与CN交于点D,由平行线的性质结合三角形的外角性质和已知条件得出∠ABN=(k+1)(∠OCH﹣∠BNQ),再由平行线的性质和已知条件得出∠HCJ=k(∠OCH﹣∠BNQ),即可得出答案.
(1)∵![]()
![]()
![]()
∴![]() ,且
,且![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵AB∥![]() 轴,
轴,![]() ,
,
∴![]() ;
;
(2)∵![]() ,
,
∴![]() ,
,
由题意得:![]() ,
,
∴![]() ,
,
∵2S△ABN≤S△BCM,
∴![]() ,
,
解得:![]() ,
,
∵当点N从点O运动到点A时,点M同时也停止运动,
∴![]() ,
,
∴t的取值范围为:![]() ;
;
(3)设AB与CN交于点D,如图所示:
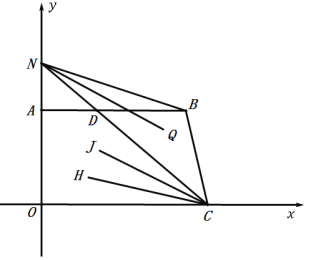
∵AB∥OC,
∴∠BDC=∠OCD,
∵∠BDC=∠BND+∠ABN,∠CNQ=k∠BNQ,∠NCH=k∠OCH,
∴∠BDC=(k+1)∠BNQ+∠ABN,∠OCD=(k+1)∠OCH,
∴(k+1)∠BNQ+∠ABN=(k+1)∠OCH,
∴∠ABN═(k+1)∠OCH﹣(k+1)∠BNQ=(k+1)(∠OCH﹣∠BNQ),
∵NQ∥CJ,
∴∠NCJ=∠CNQ=k∠BNQ,
∵∠HCJ+∠NCJ=∠NCH=k∠OCH,
∴∠HCJ=k∠OCH﹣∠NCJ=k∠OCH﹣k∠BNQ=k(∠OCH﹣∠BNQ),
∴![]() =
=![]() .
.

 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
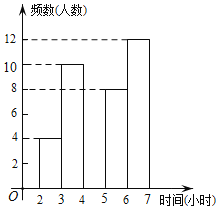
黄冈海淀全程培优测试卷系列答案【题目】某中学为了了解学生每周在校体育锻炼时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表,请根据图表信息解答下列问题:
时间(小时) | 频数(人数) | 频率 |
2≤t<3 | 4 | 0.1 |
3≤t<4 | 10 | 0.25 |
4≤t<5 | a | 0.15 |
5≤t<6 | 8 | b |
6≤t<7 | 12 | 0.3 |
合计 | 40 | 1 |
(1)表中的a= ,b= ;
(2)请将频数分布直方图补全;
(3)若该校共有1200名学生,试估计全校每周在校参加体育锻炼时间至少有4小时的学生约为多少名?