题目内容
【题目】(定义学习)
定义:如果四边形有一组对角为直角,那么我们称这样的四边形为“对直四边形”
(判断尝试)
在①梯形;②矩形:③菱形中,是“对直四边形”的是哪一个. (填序号)
(操作探究)
在菱形ABCD中,![]() 于点E,请在边AD和CD上各找一点F,使得以点A、E、C、F组成的四边形为“对直四边形”,画出示意图,并直接写出EF的长,
于点E,请在边AD和CD上各找一点F,使得以点A、E、C、F组成的四边形为“对直四边形”,画出示意图,并直接写出EF的长,

(实践应用)
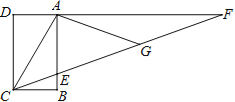
某加工厂有一批四边形板材,形状如图所示,若AB=3米,AD=1米,![]()
![]()
.现根据客户要求,需将每张四边形板材进一步分割成两个等腰三角形板材和一个“对直四边形"板材,且这两个等腰三角形的腰长相等,要求材料充分利用无剩余.求分割后得到的等腰三角形的腰长,

【答案】【判断尝试】②;【操作探究】EF的长为2,EF的长为![]() ;【实践应用】方案1:两个等腰三角形的腰长都为
;【实践应用】方案1:两个等腰三角形的腰长都为![]() 米.理由见解析,方案2:两个等腰三角形的腰长都为2米.理由见解析,方案3:两个等腰三角形的腰长都为
米.理由见解析,方案2:两个等腰三角形的腰长都为2米.理由见解析,方案3:两个等腰三角形的腰长都为![]() 米,理由见解析.方案4:两个等腰三角形的腰长都为
米,理由见解析.方案4:两个等腰三角形的腰长都为![]() 米,理由见解析.
米,理由见解析.
【解析】
[判断尝试]根据“对直四边形”定义和①梯形;②矩形:③菱形的性质逐一分析即可解答.
[操作探究]由菱形性质和30°直角三角形性质即可求得EF的长.
[实践应用]先作出“对直四边形”,容易得到另两个等腰三角形,再利用等腰三角形性质和勾股定理即可求出腰长.
解: [判断尝试]
①梯形不可能一组对角为直角;③菱形中只有正方形的一组对角为直角,②矩形四个角都是直角,故矩形有一组对角为直角,为“对直四边形”,
故答案为② ,
[操作探究]
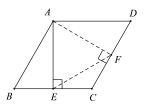
F在边AD上时,如图:
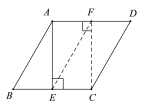
∴四边形AECF是矩形,
∴AE=CE,
又∵![]() ,
,
∴BE=1,AE=![]() ,CE=AF=1,
,CE=AF=1,
∴在Rt△AEF中,EF=![]() =2
=2
EF的长为2.
F在边CD上时,AF⊥CD,
∵四边形ABCD是菱形,
∴AB=AD=2,∠B=∠D=60°,
又∵AE⊥BC,
∴∠BAE=∠BAF=30°,
∴AE=AF=![]() ,
,
∵∠BAD=120°,
∴∠EAF=60°,
∴△AEF为等边三角形,
∴EF=AF=AE=![]()
即:EF的长为![]() ;
;
故答案为2,![]() .
.
[实践应用]
方案1:如图①,作![]() ,则四边形ABCD分为等腰
,则四边形ABCD分为等腰![]() 、等腰
、等腰![]() 、“对直四边形”ABED,其中两个等腰三角形的腰长都为
、“对直四边形”ABED,其中两个等腰三角形的腰长都为![]() 米.
米.
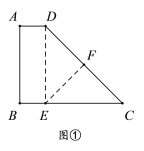
理由:![]() ,∴四边形ABED为矩形,
,∴四边形ABED为矩形,
∴![]() 3米,
3米,
∵![]() ,
,
∴△DEC为等腰直角三角形,
∴DE=EC=3米,
∴DC=![]() 米,
米,
∵![]() ,
,
∴![]() =
=![]() DC=
DC=![]() 米.
米.
方案2:如图②,作![]() ,则四边形ABCD分为等腰△FEB、等腰△FEC、“对直四边形”ABED,其中两个等腰三角形的腰长都为2米.
,则四边形ABCD分为等腰△FEB、等腰△FEC、“对直四边形”ABED,其中两个等腰三角形的腰长都为2米.
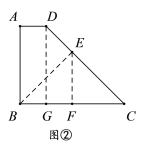
理由:作![]() ,由(1)可知
,由(1)可知![]() 3米,BG=AD=1米,
3米,BG=AD=1米,
∴BC=1+3=4米,
∵![]() ,
,
∴△BEC为等腰直角三角形,
∵![]() ,
,
∴![]()
![]() BC=2米.
BC=2米.
方案3:如图③,作CD、BC的垂直平分线交于点E,连接ED、EB,则四边形ABCD分为等腰△CED、等腰△CEB、“对直四边形”ABED,其中两个等腰三角形的腰长都为![]() 米.
米.
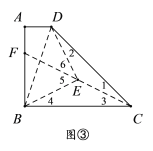
理由:连接CE,并延长交AB于点F,
∵CD、BC的垂直平分线交于点E,∴![]() ,∴
,∴![]() ,
,
∴![]()
![]() .
.
连接DB,
DB=![]() =
=![]() ,
,
∵ED=EB,
∴△BED为等腰直角三角形,
∴ED=![]() 米,
米,
∴![]()
![]() 米.
米.
方案4:如图④,作![]() ,交AB于点E,
,交AB于点E,![]() ,
,
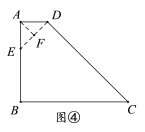
则四边形ABCD分为等腰△AFE、等腰△AFD、“对直四边形”BEDC,其中两个等腰三角形的腰长都为![]() 米.
米.
理由:作![]() ,交AB于点E,可证∠ADE
,交AB于点E,可证∠ADE![]() 45°,
45°,
∵![]() ,
,
∴△ADE为等腰直角三角形,
∴DE =![]() 米,
米,
作![]() ,
,
∴![]()
![]() DE=
DE=![]() 米.
米.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案【题目】某保健品厂每天生产A,B两种品牌的保健品共600瓶,A,B两种产品每瓶的成本和利润如下表,设每天生产A产品x瓶,生产这两种产品每天共获利y元.
A | B | |
成本(元/瓶) | 50 | 35 |
利润(元/瓶) | 20 | 15 |
(1)请求出y关于x的函数关系式;
(2)如果该厂每天至少投入成本26 400元,那么每天至少获利多少元?
(3)该厂每天生产的A,B两种产品被某经销商全部订购,厂家对A产品进行让利,每瓶利润降低![]() 元,厂家如何生产可使每天获利最大?最大利润是多少?
元,厂家如何生产可使每天获利最大?最大利润是多少?