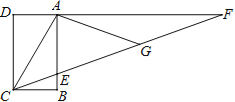
题目内容
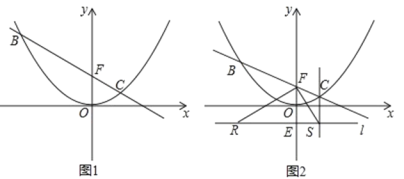
【题目】如图1所示,双曲线y=![]() (k≠0)与抛物线y=ax2+bx(a≠0)交于A、B、C三点,已知B(4,2),C(-2,-4),直线CO交双曲线于另一点D,抛物线与x轴交于另一点E.
(k≠0)与抛物线y=ax2+bx(a≠0)交于A、B、C三点,已知B(4,2),C(-2,-4),直线CO交双曲线于另一点D,抛物线与x轴交于另一点E.
(1)求双曲线和抛物线的解析式;
(2)在抛物线上是否存在点P,使得∠POE+∠BCD=90°?若存在,请求出满足条件的点P的坐标;若不存在,请说明理由;
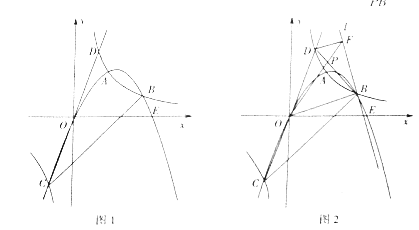
(3)如图2所示,过点B作直线L⊥OB,过点D作DF⊥L于F,BD与OF交于点P,求![]() 的值.
的值.
【答案】(1)双曲线的解析式为y=![]() ,抛物线的解析式为y=
,抛物线的解析式为y= ![]() ;(2)满足条件的P点有一个(18,-54);(3)
;(2)满足条件的P点有一个(18,-54);(3)![]()
【解析】试题分析:
(1)把点B、C的坐标分别代入反比例函数和抛物线的解析式用待定系数法即可求得两个函数的解析式了;
(2)连接BD,由点C的坐标可得直线OC的解析式为y=2x,及直线OC与![]() 的另一个交点D的坐标为(2,4),结合点B的坐标可得BC=
的另一个交点D的坐标为(2,4),结合点B的坐标可得BC=![]() ,DB=
,DB=![]() ,CD=
,CD=![]() ,由此根据勾股定理的逆定理可得∠CBD=90°及tan∠ BDC=
,由此根据勾股定理的逆定理可得∠CBD=90°及tan∠ BDC=![]() ,再证∠POE=∠BDC即可
,再证∠POE=∠BDC即可
得到tan∠POE=3,从而说明点P在直线y=3x或y=-3x上,结合点P又在抛物线上,即可分两种情况进行讨论求出点P的坐标了;
(3)如图2,由点B的坐标可得直线OB的解析式为y= ![]() ,由l⊥OB且过点B可求得l的解析式为y=-2x+10,由DF∥OB结合点D的坐标可求得直线DF的解析式为y=
,由l⊥OB且过点B可求得l的解析式为y=-2x+10,由DF∥OB结合点D的坐标可求得直线DF的解析式为y=![]() x+3,这样由l和DF的解析式可求得点F的坐标,这样就可得求得DF的长了,结合OB的长和DF∥OB即可由平行线分线段成比例求得
x+3,这样由l和DF的解析式可求得点F的坐标,这样就可得求得DF的长了,结合OB的长和DF∥OB即可由平行线分线段成比例求得![]() 的值了.
的值了.
试题解析:
(1)把B(4,2)代人y=![]() (k≠0)得2=
(k≠0)得2=![]() 元,解得k=8z,
元,解得k=8z,
∴双曲线的解析式为y=![]() ,
,
把B(4,2),C(-2,-4)代入y=ax2+bx得,
![]() ,
,
∴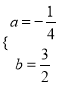 ,
,
∴抛物线的解析式为y= ![]() ;
;
(2)连接DB,
∵C(-2,-4),
∴直线OC的解析式为y=2x且与y=![]() 的另一个交点D(2,4),
的另一个交点D(2,4),
∴由两点间距离公式得BC=![]() ,DB=
,DB=![]() ,CD=
,CD=![]() ,
,
∴BC2+DB2=CD2,
∴∠CBD=90°,
∴tan∠ BDC=![]() .
.
∵∠POE+∠BCD=90°,∠BCD+∠BDC=90°,
∴∠POE=∠BDC.即tan∠POE=3.
∴P在直线y=3x或y=-3x上,故有两种情况:
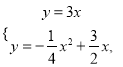
解得(0,0)(舍)或(-6,-18)(舍);
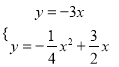 ,
,
解得(0,0)(舍)或(18,-54),
故可得出满足条件的P点有一个(18,-54);
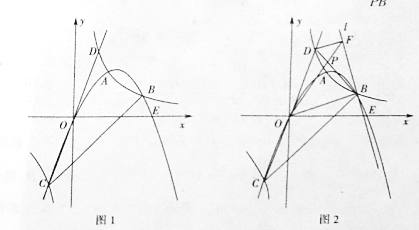
(3)由B(4,2)可得直线OB解析式y= ![]() ,
,
由OB⊥l可得l的解析式为y=-2x+b1,把(4,2)代入求出b1=10,
∴l的解析式为y=-2x+10,
由DF⊥l,OB⊥l可得DF∥OB,
∴可设DF解析式y=![]() x+b2,把D(2,4)代入得b2=3.
x+b2,把D(2,4)代入得b2=3.
∴DF的解析式为y=![]() x+3,
x+3,
把DF的解析式与l的解析式联立可得:
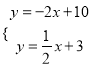 解得:
解得: 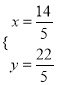 ,
,
∴![]() ,
,
∴DF= ,OB=
,OB=![]()
.∵DF∥OB,
∴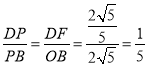 .
.

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案