题目内容
【题目】在菱形![]() 中,对角线
中,对角线![]() 与
与![]() 交于点
交于点![]() ,
,![]() ,
,![]() ,点
,点![]() 是对角线
是对角线![]() 上一点(可与
上一点(可与![]() ,
,![]() 重合),以点
重合),以点![]() 为圆心,
为圆心,![]() 为半径作
为半径作![]() (其中
(其中![]() ).
).
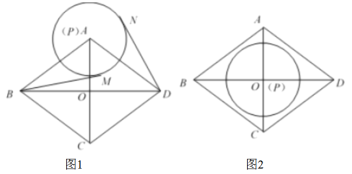
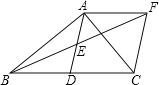
(1)如图1,当点![]() 与
与![]() 重合,且
重合,且![]() 时,过点
时,过点![]() ,
,![]() 分别作
分别作![]() 的切线,切点分别为
的切线,切点分别为![]() ,
,![]() .求证:
.求证:![]() ;
;
(2)如图2,当点![]() 与点
与点![]() 重合,且
重合,且![]() 在菱形
在菱形![]() 内部时(不含边界),求
内部时(不含边界),求![]() 的取值范围;
的取值范围;
(3)当点![]() 为
为![]() 或
或![]() 的内心时,直接写出
的内心时,直接写出![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)连接![]() ,
,![]() ,则AM=AN,根据切线的性质可得
,则AM=AN,根据切线的性质可得![]() 90°,据此通过“HL”证明Rt△BMA与Rt△DNA全等,最后利用全等三角形性质证明结论即可;
90°,据此通过“HL”证明Rt△BMA与Rt△DNA全等,最后利用全等三角形性质证明结论即可;
(2)当点![]() 与点
与点![]() 重合,
重合,![]() 在菱形内部时,过点P作
在菱形内部时,过点P作![]() 于点
于点![]() ,根据菱形的性质可得
,根据菱形的性质可得![]() ,
,![]() ,由此进一步利用勾股定理计算出
,由此进一步利用勾股定理计算出![]() ,最后通过
,最后通过![]() 结合题意进一步分析求解即可;
结合题意进一步分析求解即可;
(3)如图,当点![]() 为
为![]() 内心时,过
内心时,过![]() 作
作![]() 于
于![]() ,作
,作![]() 于
于![]() ,则有
,则有![]() ,连接
,连接![]() 、
、![]() ,根据
,根据![]() 求出此时圆的半径,从而根据
求出此时圆的半径,从而根据![]() 直接计算即可,然后当点
直接计算即可,然后当点![]() 为
为![]() 的内心时,按照相同的方法进一步求解即可.
的内心时,按照相同的方法进一步求解即可.
(1)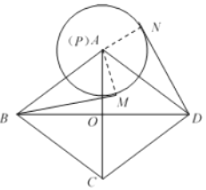
如图,连接![]() ,
,![]() ,则AM=AN,
,则AM=AN,
∵![]() ,
,![]() 分别是
分别是![]() 的切线,
的切线,
∴![]() 90°,
90°,
∵四边形ABCD是菱形,
∴AB=AD,
∴在Rt△BMA与Rt△DNA中,
∵![]() ,
,![]() ,
,
∴![]()
![]() ,
,
∴![]() ;
;
(2)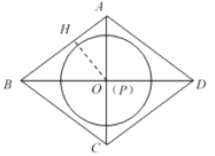
如图,当点![]() 与点
与点![]() 重合,
重合,![]() 在菱形内部时,过点P作
在菱形内部时,过点P作![]() 于点
于点![]() ,
,
![]() 在菱形
在菱形![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
由![]() ,得
,得![]() ,
,
解得:![]() ,
,
∴当点![]() 与点
与点![]() 重合,且
重合,且![]() 在菱形
在菱形![]() 内部时,
内部时,![]() 的取值范围是:
的取值范围是:![]() ;
;
(3)AP长为![]() 或
或![]() .
.
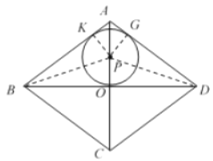
如图,当点![]() 为
为![]() 内心时,过
内心时,过![]() 作
作![]() 于
于![]() ,作
,作![]() 于
于![]() ,
,
则有![]() ,连接
,连接![]() 、
、![]() ,
,
则有![]() ,
,
由菱形性质可得:AB=AD=BC=CD=5,AO=OC=3,BO=OD=4,
∴![]() ,
,
解得:![]() ,
,
则![]() ;
;
当点![]() 为
为![]() 的内心时,同理可得
的内心时,同理可得![]() ,
,
综上所诉,![]() 或
或![]() .
.

练习册系列答案
相关题目