Question

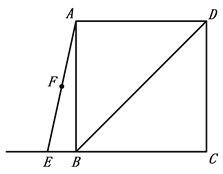
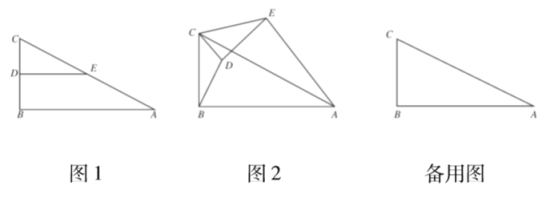
【题目】如图，在△ABC中，AB＝AC，D是AB上一点，以点D为圆心，AC为半径画弧交BA的延长线于点E，连接CD，作EF∥CD，交∠EAC的平分线于点F，连接CF．

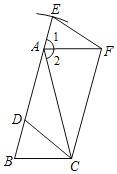
（1）求证：△BCD≌△AFE；

（2）若AC＝6，∠BAC＝30°，求四边形CDEF的面积．

Answer 1

【答案】（1）见解析；（2）四边形CDEF的面积为18．

【解析】

（1）利用三角形外角性质以及平行线的性质，可得∠B=∠1，∠BDC=∠AEF，根据ASA即可判定△BCD≌△AFE；

（2）过A作AH⊥CF，垂足为H，先判定四边形CDEF是平行四边形，即可得出CF=AB=AC=6，且CF∥AB，再根据AH=AC=3，即可得到S四边形CDEF=CF×AH=18．

解：（1）∵AB＝AC，

∴∠B＝∠ACB，

∵∠EAC＝∠B+∠ACB，

∴∠EAC＝2∠B，

∵∠1＝∠2，

∴∠EAC＝2∠1，

∴∠B＝∠1，

∵EF∥CD，

∴∠BDC＝∠AEF，

∵AB＝AC＝DE，

∴BD＝AE，

∴△BCD≌△AFE（ASA）；

（2）如图，过A作AH⊥CF，垂足为H，

∵△BCD≌△AFE，

∴CD＝EF，

又∵EF∥CD，

∴四边形CDEF是平行四边形，

∴CF＝AB＝AC＝6，且CF∥AB，

∵∠BAC＝30°，

∴∠ACH＝30°，

∴AH＝AC＝3，

∴S四边形CDEF＝CF×AH＝6×3＝18．