题目内容
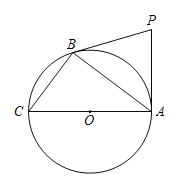
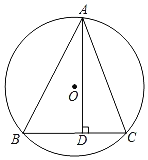
【题目】如图,![]() 内接于⊙O,∠BAC=45°,AD⊥BC,垂足为D,BD=6,DC=4.
内接于⊙O,∠BAC=45°,AD⊥BC,垂足为D,BD=6,DC=4.
(1)求⊙O的半径;
(2)求AD的长.
【答案】(1)5![]() ;(2)12
;(2)12
【解析】
(1)根据圆周角定理得到∠BOC=90°,根据等腰直角三角形的性质计算,求出OB;
(2)连接OA,过点O作OE⊥AD于E,OF⊥BC于F,根据垂径定理求出DF,根据等腰直角三角形的性质求出OF,根据勾股定理求出AE,结合图形计算得到答案.
解:(1)如图1,连接OB、OC,
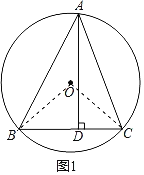
∵BD=6,DC=4,
∴BC=10,
由圆周角定理得,∠BOC=2∠BAC=90°,
∴OB=![]() BC=5
BC=5![]() ;
;
(2)如图2,连接OA,过点O作OE⊥AD于E,OF⊥BC于F,
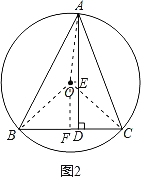
∴BF=FC=5,
∴DF=1,
∵∠BOC=90°,BF=FC,
∴OF=![]() BC=5,
BC=5,
∵AD⊥BC,OE⊥AD,OF⊥BC,
∴四边形OFDE为矩形,
∴OE=DF=1,DE=OF=5,
在Rt△AOE中,AE=![]() =7,
=7,
∴AD=AE+DE=12.

练习册系列答案
相关题目
【题目】在![]() 中,
中,![]() ,
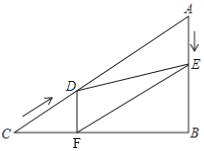
,![]() ,在图中按下列步骤进行尺规作图:
,在图中按下列步骤进行尺规作图:
① | 以 |
② | 分别以 |
③ | 画射线 |
下列说法错误的是( )
A.![]() B.
B.![]()
C.![]() D.若
D.若![]() ,则
,则![]()