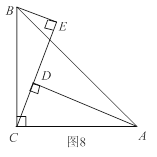
题目内容
【题目】如图8，在
中， 
， 
于
， 
于D.
（1）求证：△ADC≌△CEB. （2）
，求BE的长度.
【答案】（1）证明见解析； （2）2cm.
【解析】分析：（1）根据全等三角形的判定定理AAS推知：△ADC≌△CEB；（2）利用（1）中的全等三角形的对应边相等得到：AD=CE=5cm，CD=BE．则根据图中相关线段的和差关系得到BE=AD-DE．
解析：
(1)证明：如图,∵AD⊥CE,∠ACB=90°，
∴∠ADC=∠ACB=90°，
∴∠BCE=∠CAD(同角的余角相等).
在△ADC与△CEB中，
，
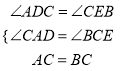∴△ADC≌△CEB(AAS)；
(2)由(1)知,△ADC≌△CEB，则AD=CE=5cm，CD=BE.
如图，∵CD=CEDE，
∴BE=ADDE=53=2(cm)，即BE的长度是2cm.
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案
相关题目
