题目内容
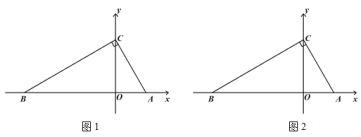
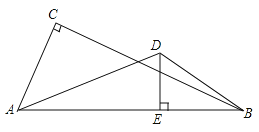
【题目】如图，学校位于高速路AB的一侧（AB成一条直线），点A，B为高速路上距学校直线距离最近的2个隧道出入口，点C、D为学校的两栋教学楼，经测量∠ACB=90°，∠ADB＞90°，AC=600m，AB=1000m，点D到高速路的最短直线距离DE=400m.
（1）求教学楼C到隧道口B的直线距离；
（2）比较AC2+BC2与AD2+BD2谁大谁小，试用计算说明.
【答案】（1）教学楼C到隧道洞口点B的直线距离为800m；（2）AD2+BD2 ＜AC2+BC2，理由见解析
【解析】
（1）在Rt△ABC中，∠C=90°，根据勾股定理，得到BC的长；
（2）①根据勾股定理，得AC2+BC2=AB2．
②过点B作BK⊥AD，交AD的延长线于点K．得BK2=BD2-DK2，BK2+AK2=AB2．（AD+DK）2+BK2=AB2．从而得到AD2+BD2＜AB2．
(1)如图，
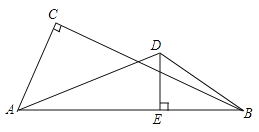
在Rt△ABC中,∠C=90°，
据勾股定理,得BC2=AB2AC2=100026002=8002.
∴BC=800(m).
即：教学楼C到隧道洞口点B的直线距离为800m
(2)AD2+BD2 ＜AC2+BC2，说理如下：如图2，
①根据勾股定理,得AC2+BC2=AB2.
②过点B作BK⊥AD，交AD的延长线于点K.
据勾股定理,得BK2=BD2DK2,BK2+AK2=AB2.
∴(AD+DK)2+BK2=AB2.
即：AD2+DK2+2ADDK+BD2DK2=AB2.
∴AD2+2ADDK+BD2=AB2.
∵AD>0，DK>0，
∴2ADDK>0
∴AD2+BD2＜AB2
综合①②,得AD2+BD2 ＜AC2+BC2
练习册系列答案
考前必练系列答案
相关题目
