题目内容
【题目】如图1,在平面直角坐标系中,点A坐标为(2,0),点B在x轴负半轴上,C在y轴正半轴上,∠ACB=90°,∠ABC=30°.
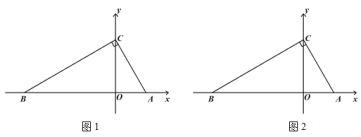
(1)求点B坐标;
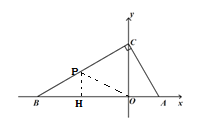
(2)如图2,点P从B出发,沿线段BC运动,点P运动速度为每秒2个单位长度,设运动时间为t秒,用含t的式子表示三角形△OBP的面积S.
【答案】(1)B(-6,0);(2)S=3t
【解析】
(1)先求出∠BAC=60°,则∠ACO=30°,再根据含30°的直角三角形得到CO的长,即可得到BO的长,故可得到B点坐标;
(2)过点P作x轴的垂线,根据题意得BP=2t,则PH=t,再根据三角形的面积即可求解;
(1)∵∠ACB=90°,∠ABC=30°.
∴∠BAC=60°,
∴∠ACO=30°,
∵点A坐标为(2,0),
∴AO=2,则AC=4,CO=![]() =2
=2![]()
∴BC=2CO=4![]() ,BO=
,BO=![]() =6,
=6,
∴B(-6,0);
(2)过点P作x轴的垂线,根据题意得BP=2t,则PH=t,
∴△OBP的面积S=![]() BO×PH=
BO×PH=![]() ×6×t=3t
×6×t=3t

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目