题目内容
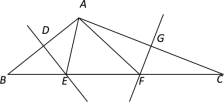
【题目】如图,在△ABC中,∠BAC=120°,若DE,FG分别垂直平分AB,AC,△AEF的周长为10cm,求BC的长及∠EAF的度数.
【答案】10;60°
【解析】
①根据线段垂直平分线的性质求出△EAF的周长证明△EAF与BC的关系从而求出BC的长度;②根据三角形内角和定理求出∠B+∠C=60°,再根据线段垂直平分线的性质求出∠BAE+∠CAF=∠B+∠C,然后求出∠EAF.
解:①∵DE,FG分别垂直平分边AB,AC,
∴EA=EB,FA=FC,
∴△EAF的周长=EA+FA+EF=BE+EF+FC=BC
∴BC=10;
②∵∠BAC=120°,
∴∠B+∠C=180°-120°=60°,
∵DE、FG分别垂直平分AB和AC,
∴∠BAE=∠B,∠CAF=∠C,
∴∠BAE+∠CAF=60°,
∴∠EAF=120°-60°=60°.
故答案为:10;60°.

练习册系列答案
相关题目