��Ŀ����
����Ŀ��һ��Բ��ֽƬ��С����������������������
![]() ��Բ��ֽƬ���Ҷ��ۣ��ۺ�ΪAB����ͼ
��Բ��ֽƬ���Ҷ��ۣ��ۺ�ΪAB����ͼ![]() ��
��
![]() ��Բ��ֽƬ�����۵���ʹA��B�����غϣ��ۺ�CD��AB�ཻ��M����ͼ
��Բ��ֽƬ�����۵���ʹA��B�����غϣ��ۺ�CD��AB�ཻ��M����ͼ![]() ��
��
![]() ��Բ��ֽƬ��EF�۵���ʹB��M�����غϣ��ۺ�EF��AB�ཻ��N����ͼ
��Բ��ֽƬ��EF�۵���ʹB��M�����غϣ��ۺ�EF��AB�ཻ��N����ͼ![]() ��
��
![]() ����AE��AF��BE��BF����ͼ
����AE��AF��BE��BF����ͼ![]() ��
��
�������ϲ�����С���õ������½��ۣ�
![]() ��
��![]() �ı���MEBF�����Σ�
�ı���MEBF�����Σ�![]() Ϊ�ȱ������Σ�
Ϊ�ȱ������Σ�![]() ��
��![]() ��
��![]() �����Ͻ�����ȷ����
�����Ͻ�����ȷ����![]()
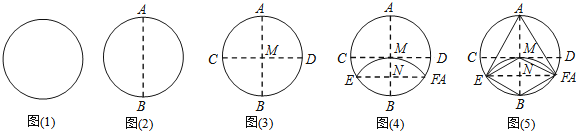
A.1��B.2��C.3��D.4��
���𰸡�D
��������
�����۵������ʿɵá�BMD=��BNF=90�㣬Ȼ������ͬλ����ȣ���ֱ��ƽ�пɵ�CD��EF���Ӷ��ж�����ȷ��
���ݴ��������ɵ�BM��ֱƽ��EF�������BN=MN���Ӷ��õ�BM��EF���ഹֱƽ�֣�Ȼ����ݶԽ����ഹֱƽ�ֵ��ı�������������ı���MEBF�����Σ��Ӷ��õ�����ȷ������ֱ��������![]() �����Ե�ֱ�DZߵ���б�ߵ�һ�������MEN=30�㣬Ȼ�������EMN=60�㣬���ݵȱ߶ԵȽ������AEM=��EAM��Ȼ�����������ε�һ����ǵ������������ڵ������ڽǵĺ������AEM=30�㣬�Ӷ��õ���AEF=60�㣬ͬ�������AFE=60�����ٸ��������ε��ڽǺ͵���180�������EAF=60�����Ӷ��ж���AEF�ǵȱ������Σ�����ȷ��
�����Ե�ֱ�DZߵ���б�ߵ�һ�������MEN=30�㣬Ȼ�������EMN=60�㣬���ݵȱ߶ԵȽ������AEM=��EAM��Ȼ�����������ε�һ����ǵ������������ڵ������ڽǵĺ������AEM=30�㣬�Ӷ��õ���AEF=60�㣬ͬ�������AFE=60�����ٸ��������ε��ڽǺ͵���180�������EAF=60�����Ӷ��ж���AEF�ǵȱ������Σ�����ȷ��
��Բ�İ뾶Ϊr�����EN= ![]() ����ɵ�EF=2EN=
����ɵ�EF=2EN=![]() �����ɵ�S�ı���AEBF��S����BEMF�Ĵ𰸣����Ԣ���ȷ��
�����ɵ�S�ı���AEBF��S����BEMF�Ĵ𰸣����Ԣ���ȷ��
�⣺��ֽƬ�����۵�A��B�����غϣ�
���BMD=90�㣬
��ֽƬ��EF�۵���B��M�����غϣ�
���BNF=90�㣬
���BMD=��BNF=90�㣬
��CD��EF���ʢ���ȷ��
���ݴ���������BM��ֱƽ��EF��
�֡�ֽƬ��EF�۵���B��M�����غϣ�
��BN=MN�� ��BM��EF���ഹֱƽ�֣�
���ı���MEBF�����Σ��ʢ���ȷ��
��ME=MB=2MN��
���MEN=30�㣬
���EMN=90��-30��=60�㣬
�֡�AM=ME�����ǰ뾶����
���AEM=��EAM��
���AEM=![]() ��EMN=
��EMN=![]() ��60��=30����
��60��=30����
���AEF=��AEM+��MEN=30��+30��=60����
ͬ�������AFE=60���� ���EAF=60����
���AEF�ǵȱ������Σ��ʢ���ȷ��
��Բ�İ뾶Ϊr����EN=![]() �� ��EF=2EN=
�� ��EF=2EN=![]() ��
��
��S�ı���AEBF��S����BEMF=![]()
�ʢ���ȷ��
����������������ȷ���Ǣ٢ڢܹۢ�4����
��ѡ��D��

 ������������ϵ�д�
������������ϵ�д�