题目内容
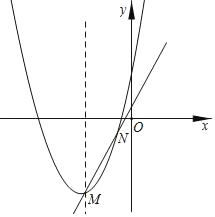
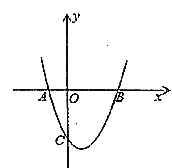
【题目】已知点P为二次函数y＝x2﹣2x﹣3图象上一点，设这个二次函数的图象与x轴交于A，B两点（A在B的右侧），与y轴交于C点，若△APC为直角三角形且AC为直角边，则点P的横坐标的值为_____．
【答案】﹣1或﹣2
【解析】
分∠ACP为直角、∠PAC为直角两种情况，利用直线与抛物线的交点求解即可．
解：对于y＝x2﹣2x﹣3①，令y＝0，则x＝3或﹣1，令x＝0，则y＝﹣3，
故点A、B、C的坐标分别为：（3，0）、（﹣1，0）、（0，﹣3）．
①当∠ACP为直角时，如下图，
由点A、C的坐标知，OA＝OC＝3，即直线AC的与x轴负半轴的夹角为45°，
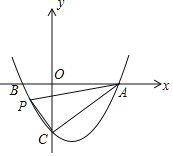
而∠ACP为直角，故直线PC的倾斜角为45°，
故设直线PC的表达式为：y＝﹣x+b，将点C的坐标代入上式并解得：b＝﹣3，
故直线PC的表达式为：y＝﹣x﹣3②，
联立①②并解得：x＝0或﹣1（舍去0），
故点P的坐标为：（﹣1，0）；
②当∠PAC为直角时，
同理可得：点P（﹣2，5）；
故答案为：﹣1或﹣2．
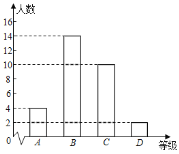
【题目】九（1）班40名学生共分为4个学习小组，数学课代表制作了1～3组学生的期中考试数学成绩频数分布表和频数分布直方图如下．余下的第4小组10名学生成绩尚未统计，这10名学生成绩如下：60，65，72，75，75，75，86，86，96，99．
1～3组频数分布表
等级 | 分数段 | 频数（人数） |
D | 60≤x＜70 | 2 |
C | 70≤x＜80 | 10 |
B | 80≤x＜90 | 14 |
A | 90≤x＜100 | 4 |
根据以上信息，解答下列问题：
（1）求第4小组10名学生成绩的众数；
（2）请你仿照数学课代表制作全班1～4组频数分布表和频数分布直方图；
1～4组频数分布表
等级 | 分数段 | 频数（人数） |
D | 60≤x＜70 |
|
C | 70≤x＜80 |
|
B | 80≤x＜90 |
|
A | 90≤x＜100 |
|
（3）全校九年级共有600名学生参加期中考试，估计该校数学成绩为A等级的学生有多少人？
