题目内容
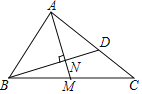
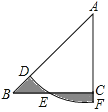
【题目】如图．在Rt△ABC中，∠ACB＝90°，AC＝BC，以A为圆心，AD长为半径的弧DF交AC的延长线于F，若图中两个阴影部分的面积相等，则
＝_____．
【答案】
【解析】
由题意，图中两个阴影部分的面积相等，则扇形ADF和△ABC的面积相等；根据等腰直角三角形的性质及面积公式分别表示出△ABC和扇形ADF的面积，变形得出AD和AB的数量关系，进而得出DB和AB的数量关系，两者相比，计算即可．
解：∵图中两个阴影部分的面积相等
∴S扇形ADF＝S△ABC
∵∠ACB＝90°，AC＝BC
∴△ABC为等腰直角三角形
∴∠A＝∠B＝45°
∴AB2＝2AC2
∵S扇形ADF＝S△ABC
∴
∴AD2＝
∴
∴
＝
∴AD＝AB
∴DB＝AB﹣AD＝（1﹣）AB
∴
＝
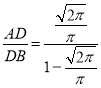故答案为：．
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
