题目内容
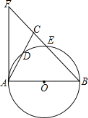
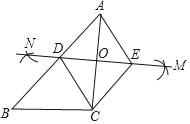
【题目】如图,在![]() 中,
中,![]() ,
,![]() 、
、![]() 的平分线分别交
的平分线分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,
,![]() 、
、![]() 相交于点
相交于点![]() ,连接
,连接![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④点
;④点![]() 到
到![]() 三个顶点的距离相等;⑤
三个顶点的距离相等;⑤![]() .其中正确的结论有( )个.
.其中正确的结论有( )个.
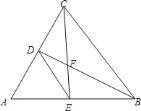
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】
利用三角形的内角和,角平分线的性质可得∠CFD=120°,所以∠BFE=60°,并且有条件易知F为三角形的内心,若想证明BE+CD=BC,只能给BE,CD找相等的线段代替,自然想到构造全等三角形.
(1)∵∠A=60°,
∴∠ABC+∠ACB=120°,
∵BD平分∠ABC,CE平分∠ACB,
∴∠ABD=∠CBD,∠ACE=∠BCE,
∴∠CBD+∠BCE=60°,
∴∠BFE=60°,
∴②cos∠BFE=![]() ,正确.
,正确.
(2)∵∠ABC,∠ACB的平分线分别交AC、AB于点D,E,CE、BD相交于点F,
∴F为三角形的内心,
∴④点F到△ABC三边的距离相等错误.
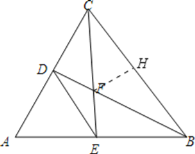
(3)在BC上截取BH=BE,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴△EBF≌△HBF,
∴∠EFB=∠HFB=60°.
由(1)知∠CFB=120°,
∴∠CFH=60°,
∴∠CFH=∠CFD=60°,
又∵CE平分∠ACB,
∴∠ACE=∠BCE,
∴△CDF≌△CHF.
∴CD=CH,
∵CH+BH=BC,
∴⑤BE+CD=BC正确.
∵△CDF≌△CFH,
∴DF=FH,
∵△FEB≌△HFB,
∴FE=FH
∵DF=FH,FE=FH,
∴DF=FE,△DEF为等腰三角形,
∴∠EDF=∠FED
故③正确.
题目现有的条件不能够证明①,所以①④错误.
故选:C.

练习册系列答案
相关题目