题目内容
【题目】如图,直线AB∥CD,点E在直线AB上,点G在直线CD上,点P在直线AB.CD之间,∠AEP=40°,∠EPG=900
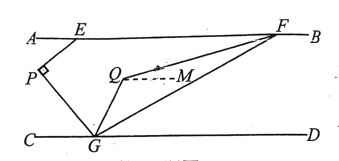
(1)填空:∠PGC=_________0;
(2)如图, 点F在直线AB上,联结FG,∠EFG的平分线与∠PGD的平分线相交于点Q,当点F在点E的右侧时,如果∠EFG=30°,求∠FQG的度数;
解:过点Q作QM∥CD
因为∠PGC+∠PGD=1800
由(1)得∠PGC=_______0,
所以∠PGD=1800-∠PGC=________0,
因为GQ平分∠PGD,
所以∠PGQ=∠QGD=![]() ∠PGD=_________0
∠PGD=_________0
(下面请补充完整求∠FQG度数的解题过程)
(3)点F在直线AB上,联结FG,∠EFG的平分线与∠PGD的平分线相交于点Q.如果∠FQG=2∠BFG,请直接写出∠EFG的度数.
【答案】(1)50;(2)∠FQG的度数为130°;(3)∠FQG的度数为98°.
【解析】
(1)延长GP交AB于点H,由AB∥CD,得∠H=∠PGC,在直角△PEH中由∠H与∠AEP互余,可求出∠H的角度,即为∠PGC的角度.
(2)过点Q作QM∥CD,由(1)结论可求∠PGD,然后由角平分线求∠QGD,再由QM∥CD求出∠MQG,由QM∥AB求出∠FQM,最后由∠FQG=∠MQG+∠FQM得出结果.
(3)设∠EFG=x°,则∠BFG=(180-x)°,由QF平分∠EFG,可得∠EFQ=![]() x°,由(2)的方法可用x表示出∠FQG,然后根据∠FQG=2∠BFG,建立方程求解.
x°,由(2)的方法可用x表示出∠FQG,然后根据∠FQG=2∠BFG,建立方程求解.
(1)如图所示,延长GP交AB于点H,因为AB∥CD,所以∠H=∠PGC,在在直角△PEH中,∠H+∠HEP=90°,所以∠H=90°-∠AEP=50°.
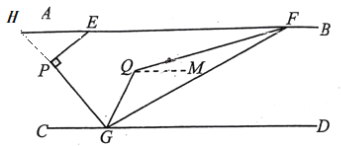
(2)过点Q作QM∥CD
因为∠PGC+∠PGD=180°
由(1)得∠PGC=50°
所以∠PGD=180°-∠PGC=130°
因为GQ平分∠PGD,
所以∠PGQ=∠QGD=![]() ∠PGD=65°
∠PGD=65°
因为QM∥CD
所以∠MQG+∠QGD=180°,则∠MQG=180°-65°=115°
又因为QM∥CD∥AB
所以∠FQM=∠EFQ
而QF平分∠EFG
所以∠EFQ=∠QFG=![]() ∠EFG=15°
∠EFG=15°
所以∠FQG=∠MQG+∠FQM=115°+15°=130°
(3)设∠EFG=x°,则∠BFG=(180-x)°,由QF平分∠EFG,可得∠EFQ=![]() x°,由(2)可知∠MQG==115°,∠FQM=∠EFQ=
x°,由(2)可知∠MQG==115°,∠FQM=∠EFQ=![]() x°,∠FQG=(115+
x°,∠FQG=(115+![]() x)°,由条件∠FQG=2∠BFG可得115+
x)°,由条件∠FQG=2∠BFG可得115+![]() x=2(180-x),解得x=98,故∠EFG的度数为98°.
x=2(180-x),解得x=98,故∠EFG的度数为98°.

 阅读快车系列答案
阅读快车系列答案