题目内容
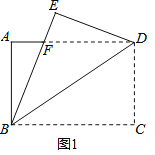
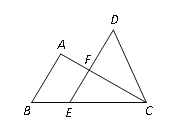
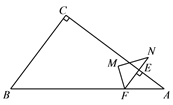
【题目】如图,在△ABC中,∠C=90°,AC=4,BC=3.点E从点A出发,以每秒4个单位长度的速度沿折线AC-CB运动,到点B停止.当点E不与△ABC的顶点重合时,过点E作其所在直角边的垂线交AB于点F,将△AEF绕点F沿逆时针方向旋转得到△NMF,使点A的对应点N落在射线FE上.设点E的运动时间为t(秒).
(1)用含t的代数式表示线段CE的长.
(2)求点M落到边BC上时t的值.
(3)当点E在边AC上运动时,设△NMF与△ABC重叠部分图形为四边形时,四边形的面积为S(平方单位),求S与t之间的函数关系式.
【答案】(1)当点E在边AC上时,![]() .当点E在边BC上时,
.当点E在边BC上时,![]() .
.
(2)![]() .(3)当
.(3)当![]() 时,
时,![]() .当
.当![]() 时,
时,![]() .
.
【解析】分析:(1)分当点E在边AC上时和当点E在边BC上时两种情况进行讨论.
(2)当点M落在边BC上时,画出示意图,![]() ,
,![]() .根据
.根据![]()
![]() .根据
.根据![]() ,列出方程求解即可.
,列出方程求解即可.
(3)分当![]() 时和当
时和当![]() 时两种情况进行讨论.
时两种情况进行讨论.
详解:(1)当点E在边AC上时,![]() .
.
当点E在边BC上时,![]() .
.
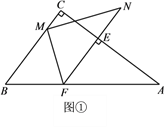
(2)如图①,当点M落在边BC上时,
![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴点M落到边BC上时t的值为![]() .
.
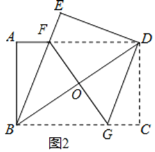
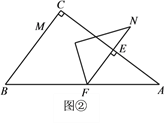
(3)当![]() 时,如图②.
时,如图②.
![]() .
.
当![]() 时,如图③.
时,如图③.
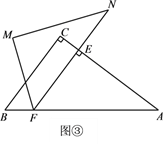
![]() .
.

练习册系列答案
相关题目