Question

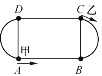
【题目】如图，点A、B、C、D把一个400米的环形跑道分成相等的4段，即两条直道和两条弯道的长度相同．甲平均每秒跑4米，乙平均每秒跑6米，若甲、乙两人分别从A、C两处同时相向出发(如图)，当他们第4次相遇时，其相遇点在____________段(填”AB”或”BC”或”CD”或”DA”)．

Answer 1

【答案】BC

【解析】甲乙两人分别从A、C两处同时相向出发，从图上可知首次相遇是个相遇问题，找到路程，知道速度，根据路程=速度×时间，可列方程求解；再次相遇仍旧是个相遇问题，找到路程，知道速度，根据路程=速度×时间，可列方程求解；找到每次相遇时间的规律，可求出相遇4次所用的时间，然后根据时间求出甲所跑的位置，从而求解．

设两人第一次相遇时跑了x秒，则有4x+6x=200，

解得：x=20，

第1次相遇，总用时20秒，

依此类推可得：

第2次相遇，总用时20+20×2，即60秒，

第3次相遇，总用时20+20×4，即100秒，

第4次相遇，总用时20+20×6，即140秒，

则此时甲跑的圈数为140×4÷400=1.4，

400×0.4=160米，

此时甲在BC弯道上，

故答案为：BC.