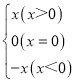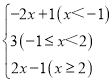题目内容
【题目】任何一个整数N，可以用一个多项式来表示:
，例如：325=3×102+2×10+5.
一个正两位数的个位数字是x，十位数字是y．
（1）把这个两位数的十位上的数字与个位上的数字交换位置得到一个新的两位数，试说明新数与原数的和能被11整除；
（2）若
试求出符合条件的所有两位数.
【答案】（1）所得的数与原数的和能被11整除（2）14、23、32、41
【解析】
（1）根据题意表示出新数与原数；
（2）根据题意表示出
、
，从而求得x+y=5，分析符合条件的x、y的值.
(1)根据题意得：10y+x+10x+y
=11（x+y），
则所得的数与原数的和能被11整除．
(2) 根据题意得：11（x+y）=55
所以x+y=5
因为0<x<5，0< y <5,且x、y为整数
所以符合条件的两位数为14、23、32、41
练习册系列答案
阅读快车系列答案
相关题目
