题目内容
【题目】已知Rt△ABC中,AC=BC,∠C=90°,D为AB边中点,∠EDF绕D点旋转,它的两边分别交AC、CB(或它们的延长线)于E、F
(1)当点E在AC边上时(如图1),求证CE=BF
(2)在(1)的条件下,求证:![]()
(3)当∠EDF绕D点旋转到图3的位置即点E、F分别在AC、CB边的延长线上时,上述(2)结论是否成立?若成立,请给予证明;若不成立,![]() 又有怎样的数量关系?请写出你的猜想,不需证明.
又有怎样的数量关系?请写出你的猜想,不需证明.

【答案】(1)答案见解析;(2)答案见解析;(3)答案见解析.
【解析】
(1)由题意证明四边形ECFD为矩形,△DFE中DF=FB,从而求解即可;(2)在图1,图2中分别进行证明,在图1中证明四边形CEDF是正方形,边长是AC的一半,即可得出结论;在图2中利用三角形全等的判定证明△CDE≌△BDF,利用中线的性质得到![]() ,从而得到
,从而得到![]() ;(3)不成立;同(2),在图3中得:△DEC≌△DBF,得出S△DEF-S△CFE=
;(3)不成立;同(2),在图3中得:△DEC≌△DBF,得出S△DEF-S△CFE=![]() S△ABC..
S△ABC..
解:
(1)由图可知:![]()
∴四边形ECFD是矩形
∴EC=DF,∠DFB=90°
∵Rt△ABC中,AC=BC,
∴![]()
∴DF=FB
∴DE=DF
∴CE=BF
(2)如图1,
∵D是AB的中点
∴AD=BD
由(1)可知![]()
∴△AED≌△DFB
∴DE=DF
∴四边形CEDF是正方形.设△ABC的边长AC=BC=a,则正方形CEDF的边长为![]() a.
a.
∴S△ABC=![]() a2,S正方形DECF=(
a2,S正方形DECF=(![]() a)2=
a)2=![]() a2
a2
即S△DEF+S△CEF=![]() S△ABC;
S△ABC;
如图2所示:连接CD;
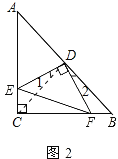
∵AC=BC,∠ACB=90°,D为AB中点,
∴∠B=45°,∠DCE=![]() ∠ACB=45°,CD⊥AB,CD=
∠ACB=45°,CD⊥AB,CD=![]() AB=BD,
AB=BD,
∴∠DCE=∠B,∠CDB=90°,
∵∠EDF=90°,
∴∠1=∠2,
在△CDE和△BDF中,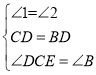 ,
,
∴△CDE≌△BDF(ASA),
∴![]()
又∵D为AB中点,
∴![]()
∴S△DEF+S△CEF=S△ADE+S△BDF=![]() S△ABC;
S△ABC;
(3)不成立;S△DEF-S△CEF=![]() S△ABC;理由如下:连接CD,
S△ABC;理由如下:连接CD,
如图3所示:
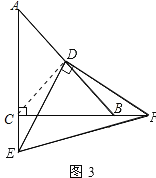
同(2)得:△DEC≌△DBF,∠DCE=∠DBF=135°
∴S△DEF=S五边形DBFEC,
=S△CFE+S△DBC,
=S△CFE+![]() S△ABC,
S△ABC,
∴S△DEF-S△CFE=![]() S△ABC.
S△ABC.
∴S△DEF、S△CEF、S△ABC的关系是:S△DEF-S△CEF=![]() S△ABC.
S△ABC.