题目内容
【题目】如图,已知二次函数y=ax2-4x+c的图象经过点A和点B.
(1)求该二次函数的表达式;
(2)写出该抛物线的对称轴及顶点坐标;
(3)点P(m,m)与点Q均在该函数图象上(其中m>0),且这两点关于抛物线的对称轴对称,求m的值及点Q到x轴的距离.
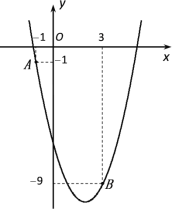
【答案】(1)二次函数的表达式为y=x2-4x-6.(2)对称轴为x=2,顶点坐标为(2,-10).(3)m=6;6.
【解析】
(1)直接利用待定系数法求出抛物线解析式;
(2)由(1)得出的抛物线解析式,配方确定出对称轴和顶点坐标;
(3)由点P(m,m)在抛物线上,确定出M的坐标,再利用对称性确定出点Q坐标即可.
(1)将x=-1、y=-1;x=3、y=-9代入y=ax2-4x+c,
得![]() ,
,
解得![]() ,
,
∴二次函数的表达式为y=x2-4x-6.
(2)∵y=x2-4x-6=(x-2)2-10,
∴对称轴为x=2,顶点坐标为(2,-10).
(3)将(m,m)代入y=x2-4x-6,得:m=m2-4m-6,
解得m1=-1,m2=6.
∵m>0,
∴m1=-1不合题意,舍去.
∴m=6.
∵点P与点Q关于对称轴x=2对称,
∴点Q到x轴的距离为6.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】甲、乙两位同学做抛骰子(均匀正方体形状)实验,他们共抛了60次,出现向上点数的次数如表:
向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现次数 | 8 | 10 | 7 | 9 | 16 | 10 |
(1)计算出现向上点数为6的频率.
(2)丙说:“如果抛600次,那么出现向上点数为6的次数一定是100次.”请判断丙的说法是否正确并说明理由.
(3)如果甲乙两同学各抛一枚骰子,求出现向上点数之和为3的倍数的概率.
【题目】某校为了解全校学生主题阅读的情况,随机抽查了部分学生在某一周主题阅读文章的篇数,并制成下列统计图表.
某校抽查的学生文章阅读的篇数统计表
文章阅读的篇数(篇) | 3 | 4 | 5 | 6 | 7 及以上 |
人数(人) | 10 | 14 | m | 8 | 6 |
请根据统计图表中的信息,解答下列问题:
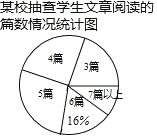
(1)求被抽查的学生人数和 m 的值;
(2) 求本次抽查的学生文章阅读篇数的中位数和众数;
(3)若该校共有 1200 名学生,根据抽查结果,估计该校学生在这一周内文章阅读的篇数为 4 篇的人数.