题目内容
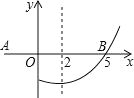
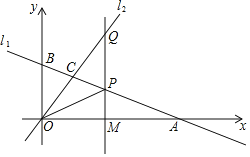
【题目】如图,直角坐标系xOy中,一次函数y=﹣![]() x+4的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(m,3),过动点M(n,0)作x轴的垂线与直线l1和l2分别交于P、Q两点.
x+4的图象l1分别与x,y轴交于A,B两点,正比例函数的图象l2与l1交于点C(m,3),过动点M(n,0)作x轴的垂线与直线l1和l2分别交于P、Q两点.
(1)求m的值及l2的函数表达式;
(2)当PQ≤4时,求n的取值范围;
(3)是否存在点P,使S△OPC=2S△OBC?若存在,求出此时点P的坐标,若不存在,请说明理由.
【答案】(1)m=2,l2的解析式为y=![]() x;(2)0≤n≤4;(3)存在,点P的坐标(6,1)或(-2,5).
x;(2)0≤n≤4;(3)存在,点P的坐标(6,1)或(-2,5).
【解析】
(1)根据待定系数法,即可求解;
(2)由l2与l1的函数解析式,可设P(n,﹣![]() n+4),Q(n,
n+4),Q(n,![]() n),结合PQ≤4,列出关于n的不等式,进而即可求解;
n),结合PQ≤4,列出关于n的不等式,进而即可求解;
(3)设P(n,﹣![]() n+4),分两种情况:①当点P在第一象限时,②当点P在第二象限时,分别列关于n的一元一次方程,即可求解.
n+4),分两种情况:①当点P在第一象限时,②当点P在第二象限时,分别列关于n的一元一次方程,即可求解.
(1)把C(m,3)代入一次函数y=﹣![]() x+4,可得:3=﹣
x+4,可得:3=﹣![]() m+4,解得:m=2,
m+4,解得:m=2,
∴C(2,3),
设l2的解析式为y=ax,则3=2a,解得a=![]() ,
,
∴l2的解析式为:y=![]() x;
x;
(2)∵PQ∥y轴,点M(n,0),
∴P(n,﹣![]() n+4),Q(n,
n+4),Q(n,![]() n),
n),
∵PQ≤4,
∴|![]() n+
n+![]() n﹣4|≤4,解得:0≤n≤4,
n﹣4|≤4,解得:0≤n≤4,
∴n的取值范围为:0≤n≤4;
(3)存在,理由如下:
设P(n,﹣![]() n+4),
n+4),
∵S△OBC=![]() ×4×2=4,S△OPC=2S△OBC,
×4×2=4,S△OPC=2S△OBC,
∴S△OPC=8,
①当点P在第一象限时,
∴S△OBP=4+8=12,
∴![]() ×4n=12,
×4n=12,
解得:n=6,
∴点P的坐标(6,1),
②当点P在第二象限时,
∴S△OBP=8-4=4,
∴![]() ×4(-n)=4,解得:n=-2,
×4(-n)=4,解得:n=-2,
∴点P的坐标(-2,5).
综上所述:点P的坐标(6,1)或(-2,5).

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目