题目内容
【题目】如图1,已知:AB∥CD,点E,F分别在AB,CD上,且OE⊥OF.
(1)求证:∠1+∠2=90°;
(2)如图2,分别在OE,CD上取点G,H,使FO平分∠CFG,EO平分∠AEH,求证:FG∥EH.
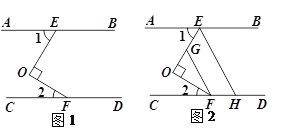
【答案】(1)证明见解析(2)证明见解析
【解析】试题分析:(1)过点O作OM∥AB,根据平行线的性质得出∠1=∠EOM,求出OM∥CD,根据平行线的性质可求解;
(2)根据平行线的性质得出∠AEH+∠CHE=180°,根据角平分线的性质和平行线的判定可求解.
试题解析:(1)方法一:过点O作OM∥AB
则∠1=∠EOM
∵AB∥CD
∴OM∥CD
∴∠2=∠FOM
∵OE⊥OF
∴∠EOF=90°,即∠EOM+∠FOM=90°
∴∠1+∠2=90°
方法二:过点F作FN∥OE交AB于N
则∠1=∠ANF,∠EOF+∠OFN=180°
∵OE⊥OF
∴∠EOF=90°
∴∠OFN=180°-∠EOF=90°
∵AB∥CD
∴∠ANF=∠NFD
∴∠1=∠NFD
∵∠1+∠OFN+∠NFD=180°
∴∠1+∠2=180°-∠OFN=90°
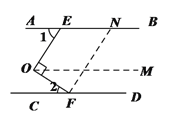
(2)∵AB∥CD
∴∠AEH+∠CHE=180°
∵FO平分∠CFG,EO平分∠AEH
∴∠CFG=2∠2,∠AEH=2∠1
∵∠1+∠2=90°
∴∠CFG+∠AEH=2∠1+2∠2=180°
∴∠CFG=∠CHE
∴FG∥EH

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目